 por DESESPERADO » Qui Nov 11, 2010 14:14
por DESESPERADO » Qui Nov 11, 2010 14:14
Olá Pessoal...estou estudando para minha prova de calculo II através da prova do semestre passado...
porém estou tendo muita dificuldade na questão abaixo...na verdade não sei ao certo o procedimento que tenho que usar...se apenas derivar ou se seria uma integral. Gostaria mt que alguem se abilitasse a me ajudar pois estou meio desperado uma vez que minha prova vai ser aplicada amanhã e tenho muita certeza que cairá uma questão como essa!
*Uma particula que se move ao longo de uma reta tem velocidade igual a

e?^-t metros por segundo após t segundos. QUal a distancia que essa particula percorre durante os t primeiro segundos?*
Podem me responder por e-mail tambem...agradeço desde já a todos que puderem contribuir.
Gabrielcoutinho13@hotmail.com
-
DESESPERADO
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Qui Nov 11, 2010 12:29
- Formação Escolar: GRADUAÇÃO
- Área/Curso: ENGENHARIA PRODUÇÃO
- Andamento: cursando
 por Neperiano » Qui Nov 11, 2010 16:29
por Neperiano » Qui Nov 11, 2010 16:29
Ola
Acho que voce deve integrar, pois segundo a fisica, se voce colocar no eixo y a velocidade e no eixo x o tempo, e traçar uma reta, curva, etc, a área desta vai ser a distância,
Para integrar ela acho que voce vai tenque usar integral por partes
Tome u = t^2
E dv = e^-t
Lembrando que para voce poder integral totalmente voce devera integral duas vezes, porque o 2 do t^2 indica quantas vezes voce vai integrar, mas se voce sabe integral por partes eu acho que vai me entender, se não souber avise aqui para que podemos mostrar
Espero ter ajudado
Atenciosamente
Sómente os mortos conhecem o fim da guerra
"Platão"
-

Neperiano
- Colaborador Voluntário

-
- Mensagens: 960
- Registrado em: Seg Jun 16, 2008 17:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
 por DESESPERADO » Qui Nov 11, 2010 17:27
por DESESPERADO » Qui Nov 11, 2010 17:27
Obrigado amigo...quanto a integração por partes realmente nao tem muito segredo
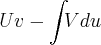
...porém me parece muito obvio apenas integrar a fórmula
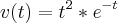
...Qual a distancia que essa particula percorre durante os t primeiros segundos?!?!...nao teria que atribuir os numeros correspondentes? ou utilizando o TFC integrar de A ate B...com base nisso quais seriam esses valores?! Obrigadooo
-
DESESPERADO
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Qui Nov 11, 2010 12:29
- Formação Escolar: GRADUAÇÃO
- Área/Curso: ENGENHARIA PRODUÇÃO
- Andamento: cursando
 por MarceloFantini » Qui Nov 11, 2010 18:07
por MarceloFantini » Qui Nov 11, 2010 18:07
Bom, suponha

e tente integrar de 0 até t. A idéia do exercício é conseguir uma expressão para o espaço em função do tempo.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por DESESPERADO » Qui Nov 11, 2010 18:23
por DESESPERADO » Qui Nov 11, 2010 18:23
SIm se for so isso acho que seria tranquilo mesmo...so pra esclarecer não teria nada a ver com essa formula nao neh?!
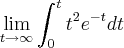
????
Estou meio sismado com essas integrais usando limites que foram muito citadas pela minha professora...mas pelo jeito nesta questão acho que não seria inviável o uso dela....mesmo pq esse infinito e meio complicado de ser encaixado numa distancia percorrida por esta particula! Desculpe o devaneio

....obrigadooo pelas colaborações!
-
DESESPERADO
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Qui Nov 11, 2010 12:29
- Formação Escolar: GRADUAÇÃO
- Área/Curso: ENGENHARIA PRODUÇÃO
- Andamento: cursando
 por MarceloFantini » Qui Nov 11, 2010 18:33
por MarceloFantini » Qui Nov 11, 2010 18:33
O limite acontece no caso de uma integral imprópria. Acho que você inclusive não deveria supor

pois é um caso particular, e fazer a integral variar de

até

, tornando-a mais geral.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por DESESPERADO » Qui Nov 11, 2010 18:41
por DESESPERADO » Qui Nov 11, 2010 18:41
realmente na hora de substituir o t por
0 e t da biziu

.......ta osso...TA pedindo a distancia que essa particula percorre durante os t primeiros segundos!!!! E a minha resposta será uma
"equação integrada"?!?! meu resultado final foi

após a integração por partes! e é isso?!?!?!


-
DESESPERADO
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Qui Nov 11, 2010 12:29
- Formação Escolar: GRADUAÇÃO
- Área/Curso: ENGENHARIA PRODUÇÃO
- Andamento: cursando
 por MarceloFantini » Qui Nov 11, 2010 18:45
por MarceloFantini » Qui Nov 11, 2010 18:45
Sim, o que há de errado? Para um determinado tempo t, a distância percorrida será essa. Se você colocar números para t, você terá um valor numérico para a distância.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por DESESPERADO » Qui Nov 11, 2010 18:46
por DESESPERADO » Qui Nov 11, 2010 18:46
DESESPERADO escreveu: meu resultado final foi

após a integração por partes! e é isso?!?!?!


errei a conta...to refazendo a integral!

-
DESESPERADO
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Qui Nov 11, 2010 12:29
- Formação Escolar: GRADUAÇÃO
- Área/Curso: ENGENHARIA PRODUÇÃO
- Andamento: cursando
 por DESESPERADO » Qui Nov 11, 2010 18:47
por DESESPERADO » Qui Nov 11, 2010 18:47
Fantini escreveu:Sim, o que há de errado? Para um determinado tempo t, a distância percorrida será essa. Se você colocar números para t, você terá um valor numérico para a distância.
uhum.....agora eu entendi.....
-
DESESPERADO
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Qui Nov 11, 2010 12:29
- Formação Escolar: GRADUAÇÃO
- Área/Curso: ENGENHARIA PRODUÇÃO
- Andamento: cursando
 por DESESPERADO » Qui Nov 11, 2010 19:28
por DESESPERADO » Qui Nov 11, 2010 19:28
Dificil mexer nesse LATEX...resolvi desta maneira e gostaria mt que alguem intervisse dizendo se fiz certo ou preciso refazer alguma conta....e tenho duvida na ultima parte....posso tirar a constante 2 e integrar somente
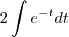
??
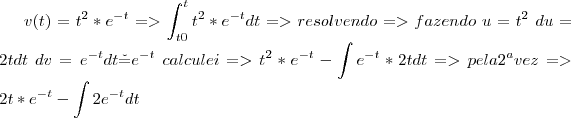
Obrigado...
-
DESESPERADO
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Qui Nov 11, 2010 12:29
- Formação Escolar: GRADUAÇÃO
- Área/Curso: ENGENHARIA PRODUÇÃO
- Andamento: cursando
 por andrefahl » Sex Nov 12, 2010 15:47
por andrefahl » Sex Nov 12, 2010 15:47
Cara, que preguiça d escreve com o LaTex mas vamo la
HAUSDhAUSDH
acho que tem alguns erros ae...

e não como antes
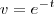
(lembre-se da regra da cadeia...)
daí a integral por partes fica

agora vc tem q resolver a segunda integral novamente por partes...
dps verifique se eu não errei em nenhum sinal, pois eh muito facil fazer confusão nessa integrais por partes...
![-2\int e^-^tdt = -t e^-^t - (\int -e^-^t dt) \Rightarrow 2\int e^-^tdt = 2[ t e^-^t - (\int e^-^t dt)]= -2\int e^-^tdt = -t e^-^t - (\int -e^-^t dt) \Rightarrow 2\int e^-^tdt = 2[ t e^-^t - (\int e^-^t dt)]=](/latexrender/pictures/09650da1bbdbb88965c332fb37659d5d.png)
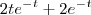
substituindo na integral anterior

onde K é uma constante arbitraria que é uma constante arbitraria.
Bom acho que seria isso =) só confiram os sinais =)
E mais uma coisa, vc tem que integrar não é por causa do que o Maligno falou dos graficos e talz da física HAUSDhUASHDUAS
pq da física vc tem que a definicão de velocidade é

por isso, como a velocidade é uma derivada do
espaço temos que o espaço é uma primitiva (integral) da velocidade =)
Att
-
andrefahl
- Usuário Dedicado

-
- Mensagens: 36
- Registrado em: Qui Out 28, 2010 18:05
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Física - UNICAMP
- Andamento: cursando
 por andrefahl » Sex Nov 12, 2010 16:44
por andrefahl » Sex Nov 12, 2010 16:44
AHSudhAUSDhaUSDH
a unica coisa foi que eu carreguei na integral o sinal negativo e o 2 dai a integral que eu resovi foi
e tem o ser essa pois na primeira parte da integração por partes vc obtem isso e não sem o 2 e o menos =)

que eh a

multiplicada por menos dois
dps eu substitui na primeira
-
andrefahl
- Usuário Dedicado

-
- Mensagens: 36
- Registrado em: Qui Out 28, 2010 18:05
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Física - UNICAMP
- Andamento: cursando
 por MarceloFantini » Sex Nov 12, 2010 17:06
por MarceloFantini » Sex Nov 12, 2010 17:06
Mas tinha esquecido o t, multiplicar o -2 depois é fácil =P.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por andrefahl » Sex Nov 12, 2010 17:45
por andrefahl » Sex Nov 12, 2010 17:45
ASDhAUSDHUASHDuAHSDUHASDuh
esqueci de escrever HAUSDhAUSD acontece
mas menos mal pq considerei nas contas =D
-
andrefahl
- Usuário Dedicado

-
- Mensagens: 36
- Registrado em: Qui Out 28, 2010 18:05
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Física - UNICAMP
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Integrar exp
por LBT » Qui Jan 13, 2011 09:05
- 4 Respostas
- 2250 Exibições
- Última mensagem por LBT

Sex Jan 14, 2011 07:03
Cálculo: Limites, Derivadas e Integrais
-
- Como integrar esta função?
por Ibraim » Ter Mar 06, 2012 17:19
- 2 Respostas
- 2777 Exibições
- Última mensagem por Ibraim

Ter Mar 06, 2012 19:00
Cálculo: Limites, Derivadas e Integrais
-
- Como integrar essa derivada: ?2/(3x²+2)dx
por Therodrigou » Ter Set 18, 2018 03:08
- 3 Respostas
- 7962 Exibições
- Última mensagem por Gebe

Ter Set 18, 2018 15:36
Cálculo: Limites, Derivadas e Integrais
-
- [Urgente] Integrar uma aceleração dada
por grey » Qua Fev 15, 2017 19:08
- 1 Respostas
- 2192 Exibições
- Última mensagem por adauto martins

Qui Fev 16, 2017 17:12
Cálculo: Limites, Derivadas e Integrais
-
- Integral indefinida - como integrar essa função?
por vinik1 » Seg Dez 05, 2011 15:53
- 2 Respostas
- 2916 Exibições
- Última mensagem por vinik1

Seg Dez 05, 2011 16:27
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 e?^-t metros por segundo após t segundos. QUal a distancia que essa particula percorre durante os t primeiro segundos?*
e?^-t metros por segundo após t segundos. QUal a distancia que essa particula percorre durante os t primeiro segundos?* 


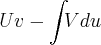 ...porém me parece muito obvio apenas integrar a fórmula
...porém me parece muito obvio apenas integrar a fórmula 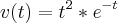 ...Qual a distancia que essa particula percorre durante os t primeiros segundos?!?!...nao teria que atribuir os numeros correspondentes? ou utilizando o TFC integrar de A ate B...com base nisso quais seriam esses valores?! Obrigadooo
...Qual a distancia que essa particula percorre durante os t primeiros segundos?!?!...nao teria que atribuir os numeros correspondentes? ou utilizando o TFC integrar de A ate B...com base nisso quais seriam esses valores?! Obrigadooo e tente integrar de 0 até t. A idéia do exercício é conseguir uma expressão para o espaço em função do tempo.
e tente integrar de 0 até t. A idéia do exercício é conseguir uma expressão para o espaço em função do tempo.

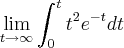 ????
???? ....obrigadooo pelas colaborações!
....obrigadooo pelas colaborações! pois é um caso particular, e fazer a integral variar de
pois é um caso particular, e fazer a integral variar de  até
até  , tornando-a mais geral.
, tornando-a mais geral. .......ta osso...TA pedindo a distancia que essa particula percorre durante os t primeiros segundos!!!! E a minha resposta será uma
.......ta osso...TA pedindo a distancia que essa particula percorre durante os t primeiros segundos!!!! E a minha resposta será uma  após a integração por partes! e é isso?!?!?!
após a integração por partes! e é isso?!?!?! 
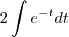 ??
??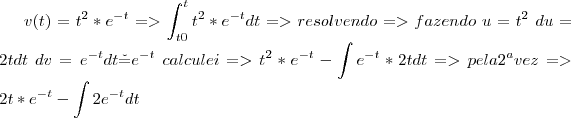
 e não como antes
e não como antes 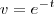 (lembre-se da regra da cadeia...)
(lembre-se da regra da cadeia...) agora vc tem q resolver a segunda integral novamente por partes...
agora vc tem q resolver a segunda integral novamente por partes...![-2\int e^-^tdt = -t e^-^t - (\int -e^-^t dt) \Rightarrow 2\int e^-^tdt = 2[ t e^-^t - (\int e^-^t dt)]= -2\int e^-^tdt = -t e^-^t - (\int -e^-^t dt) \Rightarrow 2\int e^-^tdt = 2[ t e^-^t - (\int e^-^t dt)]=](/latexrender/pictures/09650da1bbdbb88965c332fb37659d5d.png)
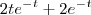
 onde K é uma constante arbitraria que é uma constante arbitraria.
onde K é uma constante arbitraria que é uma constante arbitraria. por isso, como a velocidade é uma derivada do
por isso, como a velocidade é uma derivada do 
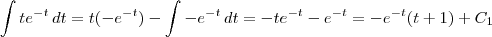
 que eh a
que eh a  multiplicada por menos dois
multiplicada por menos dois




