 por HenriquePegorari » Dom Jul 25, 2010 17:26
por HenriquePegorari » Dom Jul 25, 2010 17:26
Olá, preciso muito da ajuda sobre o método de integração por substituição, quando formos substituir por Du o que devemos fazer com a função?Derivar?
-
HenriquePegorari
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Dom Jul 25, 2010 17:09
- Formação Escolar: ENSINO FUNDAMENTAL II
- Área/Curso: Física
- Andamento: cursando
 por Molina » Seg Jul 26, 2010 14:59
por Molina » Seg Jul 26, 2010 14:59
HenriquePegorari escreveu:Olá, preciso muito da ajuda sobre o método de integração por substituição, quando formos substituir por Du o que devemos fazer com a função?Derivar?
Boa tarde, Henrique
Isso mesmo, preciso derivar as substituições que você considerar. Vou dar um exemplo para ver se fica mais fácil do que ficar passando teorias..
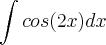
Há formulas prontas para este tipo de integração, mas o mais simples é resolver por substituição mesmo. Veja:
Se eu chamar
2x de
u, tenho que
 Derivando
Derivando de ambos os lados da igualdade...
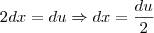
Fazendo a
substituição na nossa integral, temos que:

E agora integrar cosseno é simples...
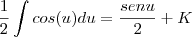
Só que minha integral é em relação a x e não a u, então faça a substituição inversa, de
u para
x...
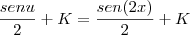
Espero ter ajudado. Qualquer coisa crie um tópico com as questões que você tiver mais dificuldades.
Bom estudo,

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por HenriquePegorari » Ter Jul 27, 2010 11:35
por HenriquePegorari » Ter Jul 27, 2010 11:35
ENTÃO DEVEMOS PRIMEIRAMENTE ESCOLHER QUAL SERÁ SUBSTITUIDO POR U E DU, DEPOIS DERIVAMOS TANTO O U QUANTO O DU, CALCULAMOS A INTEGRAL DISSO E DEPOIS PASSAMOS PARA A FORMA DE "X"
-
HenriquePegorari
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Dom Jul 25, 2010 17:09
- Formação Escolar: ENSINO FUNDAMENTAL II
- Área/Curso: Física
- Andamento: cursando
 por MarceloFantini » Ter Jul 27, 2010 12:54
por MarceloFantini » Ter Jul 27, 2010 12:54
Você faz a escolha do u, deriva e encontra
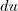
, calcula a integral e depois volta para a variável x.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Método da substituição
 por leticiapires52 » Ter Out 06, 2015 18:04
por leticiapires52 » Ter Out 06, 2015 18:04
- 2 Respostas
- 2955 Exibições
- Última mensagem por leticiapires52

Ter Out 06, 2015 20:15
Cálculo: Limites, Derivadas e Integrais
-
- [Integrais] Método da substituição
por Gabriel_1403 » Sáb Set 29, 2012 14:50
- 1 Respostas
- 1561 Exibições
- Última mensagem por MarceloFantini

Sáb Set 29, 2012 15:26
Cálculo: Limites, Derivadas e Integrais
-
- [Integral] Método da Substituição
por raimundoocjr » Sáb Jul 27, 2013 13:04
- 2 Respostas
- 2007 Exibições
- Última mensagem por raimundoocjr

Sáb Jul 27, 2013 18:02
Cálculo: Limites, Derivadas e Integrais
-
- Integração por substituição
por manuoliveira » Seg Out 22, 2012 22:33
- 2 Respostas
- 1860 Exibições
- Última mensagem por manuoliveira

Ter Out 23, 2012 00:49
Cálculo: Limites, Derivadas e Integrais
-
- integração por substituição
por medeiro_aa » Seg Dez 07, 2015 18:35
- 2 Respostas
- 3388 Exibições
- Última mensagem por medeiro_aa

Qua Mar 02, 2016 11:44
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
zig - Sex Set 23, 2011 13:57
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
Vennom - Sex Set 23, 2011 21:41
zig escreveu:![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Rpz, o negócio é o seguinte:
Quando você tem uma potência negativa, tu deve inverter a base dela. Por exemplo:

Então pense o seguinte: a fração geratriz de 0,05 é

, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
Veja:
![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
A raiz quadrada de vinte, você acha fácil, né?
Espero ter ajudado.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:23
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:24
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



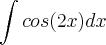

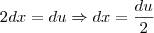

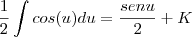
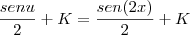



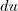 , calcula a integral e depois volta para a variável x.
, calcula a integral e depois volta para a variável x.

![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.