Eu fiz de um modo diferente do Elcioschin, mas que acredito também ser válido. O problema envolve descobrir um ponto de máximo na função que determina o volume do cone. Para simplificar, ao invés de considerar esta, eu resolvi considerar a função que determina a área do triângulo cuja rotação dá origem ao cone. É evidente que se este triângulo tiver área máxima, o cone terá volume máximo. Eis um desenho do triângulo:
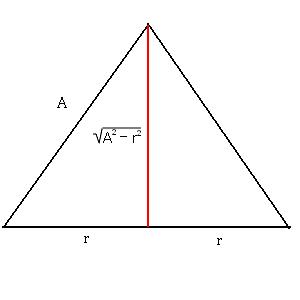
- trimatder.JPG (6.72 KiB) Exibido 2677 vezes
A área do triângulo é dada por:

Agora devemos igualar a derivada a zero para encontrarmos um ponto de máximo (ou de mínimo, ou de inflexão):
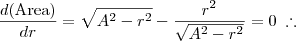
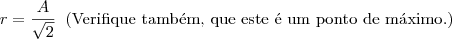
Achamos então, qual deve ser o raio, caso queiramos a área máxima. Este valor também é válido para o volume máximo. Logo:

É sempre bom verificar o gabarito, para garantir que não tenhamos errado nas contas. Até a próxima.





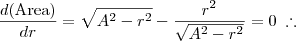
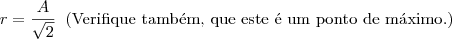

![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)