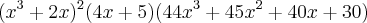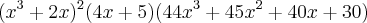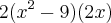por jmario » Sex Mai 07, 2010 13:51
por jmario » Sex Mai 07, 2010 13:51
Qual o resultado da seguinte derivada

Não consigo chegar no resultado do livro
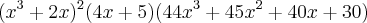
Alguém pode me ajudar como chegar nesse resultado?
-
jmario
- Usuário Dedicado

-
- Mensagens: 48
- Registrado em: Qui Abr 15, 2010 12:23
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: economia
- Andamento: formado
 por Neperiano » Sex Mai 07, 2010 14:14
por Neperiano » Sex Mai 07, 2010 14:14
Ola
Note que é uma multiplicação então deve-se se seguir a regra e alem do mais ainda tem uma função dentro da outra, que resulta em mais outra regra
Primeiro comece derivando as duas equações
Utilize u e v para ajudar
u=x
v = u^3 +2x
f(v) = v^3
Depois disso só é necessario deriva-las por suas regras, não se esqueca de substitui o u e o v,
A regra da multiplicação é
Derivada a primeira equação vezes a segunda igual mais a primeira normal vezes a derivada da segunda
Para derivar a segunda voce utiliza u tambem
u=4x+5
f(u)= u^2
Espero ter ajudado
Qualquer duvida
Atenciosamente
Sómente os mortos conhecem o fim da guerra
"Platão"
-

Neperiano
- Colaborador Voluntário

-
- Mensagens: 960
- Registrado em: Seg Jun 16, 2008 17:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
 por Elcioschin » Sex Mai 07, 2010 14:43
por Elcioschin » Sex Mai 07, 2010 14:43
f(x) = (x³ + 2x)³*(4x + 5)² ----> Regra do produto ----> f(x) = g(x)*h(x) ----> f '(x) = g(x)*h(x)' + h(x)*g(x)'
f '(x) = (x³ + 2x)³*[(4x + 5)²]' + (4x + 5)²*[(x³ + 2x)³]'
f '(x) = (x³ + 2x)³*[2*(4x + 5)*4] + (4x + 5)²*[3*(x³ + 2x)²*(3x² + 2)]
f '(x) = 8*(x³ + 2x)³*(4x + 5) + 3*(4x + 5)²*(x³ + 2x)²*(3x² + 2)
Colocando em evidência (x³ + 2x)²(4x + 5):
f '(x) = (x³ + 2x)²*(4x + 5)*[8*(x³ + 2x) + 3*(4x + 5)*(3x² + 2)]
f '(x) = (x³ + 2x)²*(4x + 5)*(8x³ + 16x + 36x³ + 45x² + 24x + 30)
f '(x) = (x³ + 2x)²*(4x + 5)*(44³ + 45x² + 40x + 30)
-
Elcioschin
- Colaborador Voluntário

-
- Mensagens: 624
- Registrado em: Sáb Ago 01, 2009 10:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: formado
 por jmario » Sex Mai 07, 2010 22:14
por jmario » Sex Mai 07, 2010 22:14
Muito obrigado
Agora eu tenho mais um a dúvida: a função é a seguinte
f(x) =

A primeira derivada dá
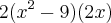
Até aí tudo bem
e a segunda derivada

Como eu chego nessa equação, eu não consigo chegar
Grato
Mario
-
jmario
- Usuário Dedicado

-
- Mensagens: 48
- Registrado em: Qui Abr 15, 2010 12:23
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: economia
- Andamento: formado
 por Elcioschin » Sex Mai 07, 2010 23:15
por Elcioschin » Sex Mai 07, 2010 23:15
Mario
A regra do fórum é postar apenas 1 questão por tópico.
Vou responder apenas porque é um problema similar.
1) Mostrei para você no problema original que tudo se resumia na Regra do Produto e simples operações algébricas.
2) O seu problema atual é similar e vc acertou na derivada primeira. Não entendo porque não sabe fazer a derivada 2ª.
Veja como é simples:
f '(x) = (4x)*(x² - 9)
f "(x) = 4x*(x² - 9)' + (x² - 9)*(4x)'
f "(x) = 4x*(2x) + (x² - 9)*(4)
f "(x) = 8x² + 4*(x² - 9) ----> Mesma coisa que f "(x) = 2*(2x)*2x) + 2*(x² - 9)*2
Qual é a sua dúvida ????
-
Elcioschin
- Colaborador Voluntário

-
- Mensagens: 624
- Registrado em: Sáb Ago 01, 2009 10:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Derivada] Ajuda com calculo de derivada de função quociente
por alienpuke » Dom Out 25, 2015 15:31
- 1 Respostas
- 12547 Exibições
- Última mensagem por Cleyson007

Dom Out 25, 2015 16:47
Cálculo: Limites, Derivadas e Integrais
-
- [Derivada]derivada de função de raiz cúbica
por armando » Sáb Jul 20, 2013 15:22
- 4 Respostas
- 14785 Exibições
- Última mensagem por armando

Dom Jul 21, 2013 22:17
Cálculo: Limites, Derivadas e Integrais
-
- [Derivada] Achar a derivada de uma função
por caiofisico » Seg Set 05, 2011 20:18
- 4 Respostas
- 3829 Exibições
- Última mensagem por caiofisico

Ter Set 06, 2011 19:44
Cálculo: Limites, Derivadas e Integrais
-
- ]Derivada de uma função] derivada com raiz
por Leandro_Araujo » Ter Mar 06, 2012 01:11
- 5 Respostas
- 8536 Exibições
- Última mensagem por LuizAquino

Ter Mar 06, 2012 13:40
Cálculo: Limites, Derivadas e Integrais
-
- Derivada de uma função
por Vitali » Qui Mai 27, 2010 11:20
- 2 Respostas
- 2156 Exibições
- Última mensagem por MarceloFantini

Qui Mai 27, 2010 18:37
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.