 por davifd_ » Qua Ago 19, 2015 10:00
por davifd_ » Qua Ago 19, 2015 10:00
Bom dia, minha dúvida é como resolver a indeterminação do limite a seguir (1/0)
- Anexos
-

- limite.jpg (7.05 KiB) Exibido 1092 vezes
-
davifd_
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Ter Ago 18, 2015 15:40
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Mecânica
- Andamento: formado
 por adauto martins » Sex Ago 21, 2015 14:39
por adauto martins » Sex Ago 21, 2015 14:39
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [limites no infinito]Limite no infinito de um ponto finito
por moyses » Ter Ago 30, 2011 12:45
- 3 Respostas
- 3528 Exibições
- Última mensagem por LuizAquino

Ter Ago 30, 2011 18:57
Cálculo: Limites, Derivadas e Integrais
-
- [Limite] Gráfico e limite para função maior inteiro
 por Raphaela_sf » Qui Abr 05, 2012 19:26
por Raphaela_sf » Qui Abr 05, 2012 19:26
- 1 Respostas
- 6645 Exibições
- Última mensagem por LuizAquino

Qui Abr 05, 2012 20:53
Cálculo: Limites, Derivadas e Integrais
-
- [Limite] Limite de funções reais de várias variáveis
por Bianca_R » Dom Nov 04, 2012 17:17
- 1 Respostas
- 4791 Exibições
- Última mensagem por MarceloFantini

Dom Nov 04, 2012 19:37
Cálculo: Limites, Derivadas e Integrais
-
- [Limite trigonométrico] Como calculo este limite?
por Ronaldobb » Qua Nov 07, 2012 23:14
- 3 Respostas
- 5120 Exibições
- Última mensagem por Ronaldobb

Qui Nov 08, 2012 07:37
Cálculo: Limites, Derivadas e Integrais
-
- [Limite] limite trigonométrico quando x tende ao infinito
por Ge_dutra » Seg Jan 28, 2013 10:13
- 2 Respostas
- 7259 Exibições
- Última mensagem por Ge_dutra

Ter Jan 29, 2013 14:20
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 7 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



 ...como
...como  e
e ![\lim_{x\rightarrow 0}senx/\sqrt[]{x}\succ \lim_{x\rightarrow 0}sen/x=1\Rightarrow \lim_{x\rightarrow 0}senx/\sqrt[]{x}=k\succ 1 \lim_{x\rightarrow 0}senx/\sqrt[]{x}\succ \lim_{x\rightarrow 0}sen/x=1\Rightarrow \lim_{x\rightarrow 0}senx/\sqrt[]{x}=k\succ 1](/latexrender/pictures/79b08da7bb514b09d4f1194fa02b7355.png) ...entao:
...entao: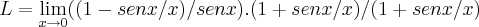 =
=![\lim_{x\rightarrow 0}(1-({sen/x})^{2}/(senx+({senx})^{2}/x)=\lim_{x\rightarrow 0}(1-({senx/x})^{2})/(senx+({senx/\sqrt[]{x}})^{2}) \lim_{x\rightarrow 0}(1-({sen/x})^{2}/(senx+({senx})^{2}/x)=\lim_{x\rightarrow 0}(1-({senx/x})^{2})/(senx+({senx/\sqrt[]{x}})^{2})](/latexrender/pictures/9f217182505326cc5f0edb0cc8e2e4ce.png)
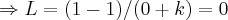

 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.