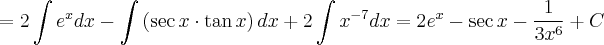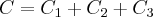1- Com o auxílio da tebela de integrais imedistas, determine a integral, a seguir:
2- Utilizando a tabela de integração imediata, o cálculo para a expressão
, resulta exatamente:
OBS: Se alguém souber algum site que posso achar a tabela de integrais imediatas.


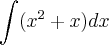
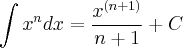
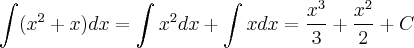
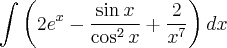
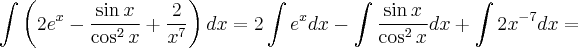
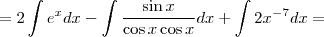
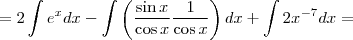
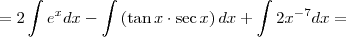
![= 2\int e^x dx -\int \left(\sec x \cdot \tan x \right) dx + 2\int x^{-7} dx \;\;\; [1] = 2\int e^x dx -\int \left(\sec x \cdot \tan x \right) dx + 2\int x^{-7} dx \;\;\; [1]](/latexrender/pictures/94bce72bbe1a2e46b413167c1e981290.png)
![\int e^{u} du = e^u + C \;\;\; [2] \int e^{u} du = e^u + C \;\;\; [2]](/latexrender/pictures/6ce11cd3eff73e310096795a5c15a5d0.png)
![\int (\sec u \tan u) dx = \sec u + C \;\;\; [3] \int (\sec u \tan u) dx = \sec u + C \;\;\; [3]](/latexrender/pictures/7655028a94ce463bba2dd6c871a4dce7.png)
![\int x^n dx = \frac{x^{(n+1)}}{n+1} + C \;\;\; [4] \int x^n dx = \frac{x^{(n+1)}}{n+1} + C \;\;\; [4]](/latexrender/pictures/d652b63db9046e6fe3de2671c6a23eec.png)
![2\int e^x dx = 2 \cdot(e^x) + {C}_{1} \;\;\;\;\; [5] 2\int e^x dx = 2 \cdot(e^x) + {C}_{1} \;\;\;\;\; [5]](/latexrender/pictures/39e4a420a000fda9236fbcabba6400cc.png)
![\int \left(\sec x \cdot \tan x \right) dx = \sec x + {C}_{2} \;\;\;\;\; [6] \int \left(\sec x \cdot \tan x \right) dx = \sec x + {C}_{2} \;\;\;\;\; [6]](/latexrender/pictures/3165f7886af07f0dc8f11c2a204b6b17.png)
![2\int x^{-7} dx = 2 \cdot \left(\frac{{x}^{-7 + 1}}{-7+1} \right) + {C}_{3} = 2 \cdot \left(\frac{{x}^{-6}}{-6} \right) + {C}_{3} = -\frac{1}{3{x}^{6}} + {C}_{3} \;\;\;\;\; [7] 2\int x^{-7} dx = 2 \cdot \left(\frac{{x}^{-7 + 1}}{-7+1} \right) + {C}_{3} = 2 \cdot \left(\frac{{x}^{-6}}{-6} \right) + {C}_{3} = -\frac{1}{3{x}^{6}} + {C}_{3} \;\;\;\;\; [7]](/latexrender/pictures/0a7ddaa798f7ba9bb7b714f5d47366a3.png)