 por Rosi7 » Sex Ago 07, 2015 21:34
por Rosi7 » Sex Ago 07, 2015 21:34
Gente não estou conseguindo fazer a multiplicação de forma correta, a questão é que mesmo fazendo de forma incorreta minha resposta está batendo com a do livro, pois sempre chego em um numero 1/infinito embaixo = 0, porém tem algo errado.. Eu sinto que tem algo, igual uma questão anterior que eu cortava tudo.. PS: Estou resolvendo o livro leithold por conta própria, não sei ao certo quantas vezes tentei fazer esta questão, mas foram vária e o máximo que chego é na resposta final zero. Embora eu não entendo o que faço na multiplicação, apenas estou usando (a^3-b^3) = a^2 + ab + b^2.
PS: Não posso usar derivada, estou em calculo I e só posso usa-lo na 3 unidade.. ou seja. Se alguém puder me ajudar, peço que seja no tradicional.
![\lim_{-\infty}\sqrt[3]{{x}^{3} + x} - \sqrt[3]{{x}^{3} + 1} \lim_{-\infty}\sqrt[3]{{x}^{3} + x} - \sqrt[3]{{x}^{3} + 1}](/latexrender/pictures/add83a736a8abbc584a6bea31b918fd8.png)
-
Rosi7
- Usuário Ativo

-
- Mensagens: 15
- Registrado em: Sáb Mai 02, 2015 18:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Física
- Andamento: cursando
 por nakagumahissao » Sáb Ago 08, 2015 12:54
por nakagumahissao » Sáb Ago 08, 2015 12:54
Eu faço a diferença. E você?
Do Poema: Quanto os professores "fazem"?
De Taylor Mali
-
nakagumahissao
- Colaborador Voluntário

-
- Mensagens: 386
- Registrado em: Qua Abr 04, 2012 14:07
- Localização: Brazil
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Lic. Matemática
- Andamento: cursando
-
 por Rosi7 » Seg Ago 10, 2015 13:22
por Rosi7 » Seg Ago 10, 2015 13:22
Entendi onde é meu erro. Embaixo eu não repetia, fiz a regra do a² +ab + b² também.. Que confusão a minha!!!
Muitíssimo obrigada!!!!!!!!
Obs: Nakagumahissao, notei que você usou a²-b², posso usar isso? Sendo que tenho raiz cúbica o certo não seria a³-b³?
-
Rosi7
- Usuário Ativo

-
- Mensagens: 15
- Registrado em: Sáb Mai 02, 2015 18:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Física
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Limite raiz cúbica
por Carolminera » Qua Jul 16, 2014 18:25
- 0 Respostas
- 3552 Exibições
- Última mensagem por Carolminera

Qua Jul 16, 2014 18:25
Cálculo: Limites, Derivadas e Integrais
-
- Limite de função com raiz cúbica
por leandroassisc » Ter Mar 10, 2015 16:25
- 3 Respostas
- 3021 Exibições
- Última mensagem por leandroassisc

Ter Mar 10, 2015 20:59
Cálculo: Limites, Derivadas e Integrais
-
- Limite com raíz cubica sendo o denominador x
por danivelosor » Sáb Mar 28, 2015 21:49
- 1 Respostas
- 2491 Exibições
- Última mensagem por DanielFerreira

Sáb Abr 04, 2015 18:48
Cálculo: Limites, Derivadas e Integrais
-
- (Limite) tendendo a - infinito com raiz cúbica
por kAKO » Qui Mai 07, 2015 12:18
- 1 Respostas
- 4425 Exibições
- Última mensagem por adauto martins

Sáb Mai 09, 2015 15:46
Cálculo: Limites, Derivadas e Integrais
-
- [Raiz Cúbica e Raiz Quadrada] Muito difícil achar a solução.
por Leocondeuba » Sáb Mai 11, 2013 19:27
- 2 Respostas
- 7448 Exibições
- Última mensagem por Leocondeuba

Sáb Mai 11, 2013 20:42
Aritmética
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\lim_{-\infty}\sqrt[3]{{x}^{3} + x} - \sqrt[3]{{x}^{3} + 1} \lim_{-\infty}\sqrt[3]{{x}^{3} + x} - \sqrt[3]{{x}^{3} + 1}](/latexrender/pictures/add83a736a8abbc584a6bea31b918fd8.png)

![\lim_{-\infty}\sqrt[3]{{x}^{3} + x} - \sqrt[3]{{x}^{3} + 1} \lim_{-\infty}\sqrt[3]{{x}^{3} + x} - \sqrt[3]{{x}^{3} + 1}](/latexrender/pictures/add83a736a8abbc584a6bea31b918fd8.png)

![\lim_{x \rightarrow \infty}\sqrt[3]{{x}^{3} + x} - \sqrt[3]{{x}^{3} + 1} \lim_{x \rightarrow \infty}\sqrt[3]{{x}^{3} + x} - \sqrt[3]{{x}^{3} + 1}](/latexrender/pictures/f4bf528771ff5db053bc84b3b21cef39.png)
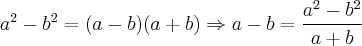


![\lim_{x \rightarrow \infty} \sqrt[3]{{x}^{3} + x} - \sqrt[3]{{x}^{3} + 1} = \lim_{x \rightarrow \infty} \frac{\left(\sqrt[3]{{x}^{3} + x} \right)^{2} - \left(\sqrt[3]{{x}^{3} + 1} \right)^2}{\sqrt[3]{{x}^{3} + x} + \sqrt[3]{{x}^{3} + 1}} = \lim_{x \rightarrow \infty} \sqrt[3]{{x}^{3} + x} - \sqrt[3]{{x}^{3} + 1} = \lim_{x \rightarrow \infty} \frac{\left(\sqrt[3]{{x}^{3} + x} \right)^{2} - \left(\sqrt[3]{{x}^{3} + 1} \right)^2}{\sqrt[3]{{x}^{3} + x} + \sqrt[3]{{x}^{3} + 1}} =](/latexrender/pictures/9114dfce4b39f8b7cd2906ffb763bb75.png)
![= \lim_{x \rightarrow \infty} \frac{\left(x\sqrt[3]{1 + \frac{x}{{x}^{3}}} \right)^{2} - \left(x\sqrt[3]{1 + \frac{1}{{x}^{3}}} \right)^2}{x\sqrt[3]{1 + \frac{x}{{x}^{3}}} + x\sqrt[3]{1 + \frac{1}{{x}^{3}}}} = \frac{x^2 - x^2}{x + x} = \frac{0}{2x} = 0 = \lim_{x \rightarrow \infty} \frac{\left(x\sqrt[3]{1 + \frac{x}{{x}^{3}}} \right)^{2} - \left(x\sqrt[3]{1 + \frac{1}{{x}^{3}}} \right)^2}{x\sqrt[3]{1 + \frac{x}{{x}^{3}}} + x\sqrt[3]{1 + \frac{1}{{x}^{3}}}} = \frac{x^2 - x^2}{x + x} = \frac{0}{2x} = 0](/latexrender/pictures/3e05918d967686c6e2124bdad75c835f.png)
![\sqrt[3]{{x}^{3} + x} = \sqrt[3]{\frac{{x}^{3}}{{x}^{3}}({x}^{3} + x)} = \sqrt[3]{{x}^{3} \left(1 + \frac{x}{x^3} \right)} = \sqrt[3]{{x}^{3} + x} = \sqrt[3]{\frac{{x}^{3}}{{x}^{3}}({x}^{3} + x)} = \sqrt[3]{{x}^{3} \left(1 + \frac{x}{x^3} \right)} =](/latexrender/pictures/ad36237a883c4a379b92790cb4478964.png)
![= \sqrt[3]{{x}^{3} } \cdot \sqrt[3]{\left(1 + \frac{x}{x^3} \right)} = x\sqrt[3]{\left(1 + \frac{x}{x^3} \right)} = \sqrt[3]{{x}^{3} } \cdot \sqrt[3]{\left(1 + \frac{x}{x^3} \right)} = x\sqrt[3]{\left(1 + \frac{x}{x^3} \right)}](/latexrender/pictures/728277bb54a4c41e044fe225d32f88f0.png)


