Preciso de ajuda para resolver o seguinte exercício: "Um fio de comprimento L é cortado em dois pedaços, um dos quais formará um círculo e o outro, um quadrado. Como deve ser cortado o fio para que a soma das áreas do círculo e do quadrado seja máxima?"
Minha resolução:
Seja x o pedaço de L destinado ao círculo. Seja y, o do quadrado. Temos x + y = L. Sabemos que a área de um círculo é dada por:
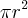, onde r é o raio. Como temos o comprimento x, vem que 
. Logo, 
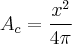é a área do círculo. Da mesma forma, temos que a área do quadrado é dada por: 
, onde 
é a medida do lado do quadrado. Mas, sabemos que 
. Logo, 
. Para trabalharmos com uma variável, segue: 
. Substituindo, vem que: 
. Somando as duas áreas, temos: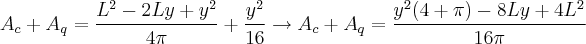 
. Derivando, temos: 
. Daí, fazendo um estudo do sinal, não encontrei ponto de máximo, e, sim, de mínimo.Por favor, preciso de ajuda! Muito Obrigada!
por