1 - Seja
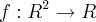 e suponha que fx(x,y) = 0 e fy(x,y)=0, PARA TODO (x,y) pertencente ao
e suponha que fx(x,y) = 0 e fy(x,y)=0, PARA TODO (x,y) pertencente ao 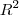 , prove que f é uma constante.
, prove que f é uma constante.b) Dê um exemplo de uma função f:A -> R^2 tal que fx(x,y) = 0 e fy(x,y)=0, para todo (x,y) pertencente a 'A', mas que f não seja constante em A.


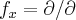 f/x...
f/x... ...o mesmo faz-se com
...o mesmo faz-se com 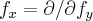 ...
...


 .
.
 :
: