 por Carolminera » Seg Jul 21, 2014 18:13
por Carolminera » Seg Jul 21, 2014 18:13
Seja f: R -> R uma função diferenciável em um ponto a E R(reais). Calcule, em termos de f ' (a), o limite:
![\lim_{x -> 0} \frac{f(x)- f(a)}{\sqrt[]{x} - \sqrt[]{a}} \lim_{x -> 0} \frac{f(x)- f(a)}{\sqrt[]{x} - \sqrt[]{a}}](/latexrender/pictures/36f9bb2a2b9d469cf23a3bbe7f8fe54d.png)
Alguém pode me ajudar?
Obrigada desde já!
-
Carolminera
- Usuário Ativo

-
- Mensagens: 19
- Registrado em: Qua Jul 02, 2014 15:57
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Física Médica
- Andamento: cursando
 por e8group » Ter Jul 22, 2014 01:48
por e8group » Ter Jul 22, 2014 01:48
Dica :
Multiplique em cima e em baixo por

e dps utilize regra operatória limites .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Carolminera » Ter Jul 22, 2014 10:41
por Carolminera » Ter Jul 22, 2014 10:41
Poderia demonstrar como fica? É que eu realmente não estou entendendo como fazer a operação, o exercício para mim está meio confuso.
-
Carolminera
- Usuário Ativo

-
- Mensagens: 19
- Registrado em: Qua Jul 02, 2014 15:57
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Física Médica
- Andamento: cursando
 por e8group » Ter Jul 22, 2014 11:23
por e8group » Ter Jul 22, 2014 11:23
Primeiro traduzimos a hipótese na linguagem dos limites ...
Dizer que f é diferenciável em um ponto

implica em dizer que o limite
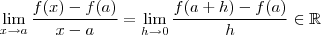
existe e uma notação para designar esta afirmação é

.
Agora note que desejamos computar o limite

. Nosso objetivo é escrever
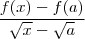
como

(tal que
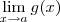
existe ) para que possamos aplicar a regra operatória do produto (vide livros de cálculo 1) .
Utilizando que

, nós temos que
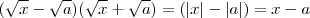
(estar implícito a positividade de

) (*) .
Como sugerir ... ( no primeiro membro estamos multiplicando por uma quantidade não nula e dividindo pela mesma quantidade , estamos trabalhando com x mt próximo de a , mas differente de a ; no segundo membro usamos o resultado marcado por (*) ) o limite desejado equivale a calcular o seguinte limite
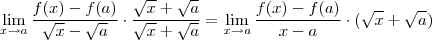
.
Tendo em conta que ambos limites abaixo existem ,
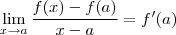
(hipótese )

, então podemos aplicar a regra operatória do produto para obter

.
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Limite] Gráfico e limite para função maior inteiro
 por Raphaela_sf » Qui Abr 05, 2012 19:26
por Raphaela_sf » Qui Abr 05, 2012 19:26
- 1 Respostas
- 6645 Exibições
- Última mensagem por LuizAquino

Qui Abr 05, 2012 20:53
Cálculo: Limites, Derivadas e Integrais
-
- [Limite] Limite de funções reais de várias variáveis
por Bianca_R » Dom Nov 04, 2012 17:17
- 1 Respostas
- 4791 Exibições
- Última mensagem por MarceloFantini

Dom Nov 04, 2012 19:37
Cálculo: Limites, Derivadas e Integrais
-
- [Limite trigonométrico] Como calculo este limite?
por Ronaldobb » Qua Nov 07, 2012 23:14
- 3 Respostas
- 5120 Exibições
- Última mensagem por Ronaldobb

Qui Nov 08, 2012 07:37
Cálculo: Limites, Derivadas e Integrais
-
- [Limite] limite trigonométrico quando x tende ao infinito
por Ge_dutra » Seg Jan 28, 2013 10:13
- 2 Respostas
- 7260 Exibições
- Última mensagem por Ge_dutra

Ter Jan 29, 2013 14:20
Cálculo: Limites, Derivadas e Integrais
-
- [Limite] Limite de funções piso (maior inteiro)
por ViniciusAlmeida » Sáb Fev 14, 2015 10:09
- 2 Respostas
- 4437 Exibições
- Última mensagem por adauto martins

Qui Fev 19, 2015 15:01
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 5 visitantes
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\lim_{x -> 0} \frac{f(x)- f(a)}{\sqrt[]{x} - \sqrt[]{a}} \lim_{x -> 0} \frac{f(x)- f(a)}{\sqrt[]{x} - \sqrt[]{a}}](/latexrender/pictures/36f9bb2a2b9d469cf23a3bbe7f8fe54d.png)

![\lim_{x -> 0} \frac{f(x)- f(a)}{\sqrt[]{x} - \sqrt[]{a}} \lim_{x -> 0} \frac{f(x)- f(a)}{\sqrt[]{x} - \sqrt[]{a}}](/latexrender/pictures/36f9bb2a2b9d469cf23a3bbe7f8fe54d.png)

 e dps utilize regra operatória limites .
e dps utilize regra operatória limites .

 implica em dizer que o limite
implica em dizer que o limite 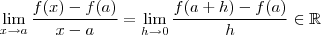 existe e uma notação para designar esta afirmação é
existe e uma notação para designar esta afirmação é  .
.  . Nosso objetivo é escrever
. Nosso objetivo é escrever 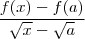 como
como  (tal que
(tal que 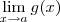 existe ) para que possamos aplicar a regra operatória do produto (vide livros de cálculo 1) .
existe ) para que possamos aplicar a regra operatória do produto (vide livros de cálculo 1) .  , nós temos que
, nós temos que 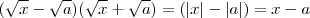 (estar implícito a positividade de
(estar implícito a positividade de  ) (*) .
) (*) . 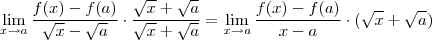 .
.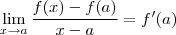 (hipótese )
(hipótese )  , então podemos aplicar a regra operatória do produto para obter
, então podemos aplicar a regra operatória do produto para obter  .
.


 substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.