 por Janoca » Sex Jun 06, 2014 17:24
por Janoca » Sex Jun 06, 2014 17:24
Por favor, ajudem-me responder essa questão, não consigo resolve-la.
Se x e y são medidos em metros, a área da região entre as curvas
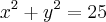
e
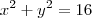
é igual a quanto? tento resolver, mas não da certo.
-
Janoca
- Usuário Dedicado

-
- Mensagens: 30
- Registrado em: Sex Jun 06, 2014 16:47
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matemática
- Andamento: cursando
 por alienante » Dom Jun 15, 2014 13:24
por alienante » Dom Jun 15, 2014 13:24
-
alienante
- Usuário Dedicado

-
- Mensagens: 43
- Registrado em: Seg Nov 25, 2013 19:18
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por Janoca » Dom Jun 15, 2014 20:30
por Janoca » Dom Jun 15, 2014 20:30
Boa noite Alienante, em relação a esta questão me ensinaram desta maneira, está correto?
![\int_{5}^{4}\sqrt[]{25-x^2}dx + \int_{0}^{4}(\sqrt[]{25-x^2}-\sqrt[]{16-x^2})dx \int_{5}^{4}\sqrt[]{25-x^2}dx + \int_{0}^{4}(\sqrt[]{25-x^2}-\sqrt[]{16-x^2})dx](/latexrender/pictures/4e5fa4eab954d480f30fc54f38ad5325.png)
-
Janoca
- Usuário Dedicado

-
- Mensagens: 30
- Registrado em: Sex Jun 06, 2014 16:47
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matemática
- Andamento: cursando
 por alienante » Dom Jun 15, 2014 20:51
por alienante » Dom Jun 15, 2014 20:51
muito incompleto.Essa integral só representa um quarto da área total, ao meu ver. Veja se observarmos os intervalos de integração de
![[0,5] [0,5]](/latexrender/pictures/be66a98c7ffb0b7cd18378674ce90c9c.png)
,do jeito que foi montado,esse calculo só nos mostra a área do primeiro quadrante, ignorando completamente os segundo,terceiro e quarto quadrantes.
-
alienante
- Usuário Dedicado

-
- Mensagens: 43
- Registrado em: Seg Nov 25, 2013 19:18
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por Janoca » Dom Jun 15, 2014 21:16
por Janoca » Dom Jun 15, 2014 21:16
em relação a sua resposta, pq vc coloca o dois na frente das raizes?
-
Janoca
- Usuário Dedicado

-
- Mensagens: 30
- Registrado em: Sex Jun 06, 2014 16:47
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matemática
- Andamento: cursando
 por alienante » Dom Jun 15, 2014 21:42
por alienante » Dom Jun 15, 2014 21:42
Porque considero tanto as áreas do primeiro e segundo quadrantes quanto as do terceiro e do quarto. Que por sinal valem a mesma coisa que as do primeiro e segundo quadrantes.
-
alienante
- Usuário Dedicado

-
- Mensagens: 43
- Registrado em: Seg Nov 25, 2013 19:18
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Duvida para achar Area entre curvas
por gabrielnandi » Qua Mai 30, 2012 18:23
- 4 Respostas
- 3365 Exibições
- Última mensagem por gabrielnandi

Seg Jun 18, 2012 01:40
Cálculo: Limites, Derivadas e Integrais
-
- Integrais e área entre curvas
 por Victor Mello » Ter Nov 19, 2013 21:58
por Victor Mello » Ter Nov 19, 2013 21:58
- 2 Respostas
- 2020 Exibições
- Última mensagem por Victor Mello

Qua Nov 20, 2013 00:28
Cálculo: Limites, Derivadas e Integrais
-
- Área entre curvas. Sen(x) e x³ em [0, pi]. Alguém ajuda?
por vmoura » Dom Abr 02, 2017 17:56
- 0 Respostas
- 3045 Exibições
- Última mensagem por vmoura

Dom Abr 02, 2017 17:56
Cálculo: Limites, Derivadas e Integrais
-
- Integral, área da região limitada.
por Maicon Simoes » Qui Abr 19, 2012 10:58
- 1 Respostas
- 1938 Exibições
- Última mensagem por LuizAquino

Qui Abr 19, 2012 15:00
Cálculo: Limites, Derivadas e Integrais
-
- [Integral dupla ƒƒ] área de região
por ricardosanto » Sex Nov 02, 2012 12:05
- 1 Respostas
- 1811 Exibições
- Última mensagem por young_jedi

Sex Nov 02, 2012 17:12
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
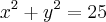 e
e 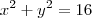 é igual a quanto? tento resolver, mas não da certo.
é igual a quanto? tento resolver, mas não da certo.
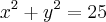 e
e 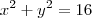 é igual a quanto? tento resolver, mas não da certo.
é igual a quanto? tento resolver, mas não da certo.

![\int_{5}^{4}\sqrt[]{25-x^2}dx + \int_{0}^{4}(\sqrt[]{25-x^2}-\sqrt[]{16-x^2})dx \int_{5}^{4}\sqrt[]{25-x^2}dx + \int_{0}^{4}(\sqrt[]{25-x^2}-\sqrt[]{16-x^2})dx](/latexrender/pictures/4e5fa4eab954d480f30fc54f38ad5325.png)

![[0,5] [0,5]](/latexrender/pictures/be66a98c7ffb0b7cd18378674ce90c9c.png) ,do jeito que foi montado,esse calculo só nos mostra a área do primeiro quadrante, ignorando completamente os segundo,terceiro e quarto quadrantes.
,do jeito que foi montado,esse calculo só nos mostra a área do primeiro quadrante, ignorando completamente os segundo,terceiro e quarto quadrantes.


 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
