 por lucasAS » Dom Jun 01, 2014 16:44
por lucasAS » Dom Jun 01, 2014 16:44
\int\limits_{-3}^{3}(\sqrt{9-x^2}+x^{13}e^{2x+1}+cos(3x-6)-sen(4x)+\frac{x}{(x^2+1)(x^2+2)}dx
Sei que pode afirmar q varias dessa integrais sao 0.. e calcular apenas algumas.. mas n sei como fazer isso,nen quais cortar..
Se puderem me explicar..
Obrigado !
-
lucasAS
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Sáb Mai 31, 2014 19:06
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
 por e8group » Qua Jun 04, 2014 16:00
por e8group » Qua Jun 04, 2014 16:00
Proposição :
Se

é uma função impar integrável em um intervalo fechado cujos os extremos do intervalo são números simétricos , então a integral de f sobre este intervalo vale zero .
Lembrando que f é impar se ocorrer x ,-x estão em Dom(f) e f(x) = -f(-x) .
Por simplicidade , vamos "chamar" a própria regra de associação ou lei de formação , da função f , de função . Assim, vamos dizer a função f(x) ...
Do integrando , a segunda e as duas ultimas 'funções ' são impares (em ordem da esquerda para a direita)[deixo vc verificar este fato !] e estas 'funções ' são continuas no intervalo
![[-3,3] [-3,3]](/latexrender/pictures/083d33f8040330c3051e16ce69a5b0df.png)
e portanto integrável sobre este intervalo .Graças a proposição acima , o integral sobre
![[-3,3] [-3,3]](/latexrender/pictures/083d33f8040330c3051e16ce69a5b0df.png)
destas 'funções ' valem zero . Usando a linearidade da integral , as contas se resumem a
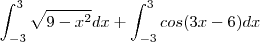
.
Consegue avançar ??
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Alguém sabe calcular essa Integral ?e?.senxdx ?
por lucat28 » Qua Mar 16, 2011 12:43
- 2 Respostas
- 2408 Exibições
- Última mensagem por lucat28

Qua Mar 16, 2011 17:35
Cálculo: Limites, Derivadas e Integrais
-
- Como resolver essa integral.
por 380625 » Qua Set 07, 2011 14:02
- 3 Respostas
- 3107 Exibições
- Última mensagem por Neperiano

Qua Set 07, 2011 15:37
Cálculo: Limites, Derivadas e Integrais
-
- Como resolvo essa integral indefinida??
por Justiceira » Sáb Out 31, 2009 19:52
- 3 Respostas
- 3063 Exibições
- Última mensagem por Molina

Seg Nov 23, 2009 21:06
Cálculo: Limites, Derivadas e Integrais
-
- Integral indefinida - como integrar essa função?
por vinik1 » Seg Dez 05, 2011 15:53
- 2 Respostas
- 2916 Exibições
- Última mensagem por vinik1

Seg Dez 05, 2011 16:27
Cálculo: Limites, Derivadas e Integrais
-
- [Integral] como calcular
por ghiza » Seg Jul 15, 2013 11:23
- 2 Respostas
- 1787 Exibições
- Última mensagem por ghiza

Seg Jul 15, 2013 13:24
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
zig - Sex Set 23, 2011 13:57
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
Vennom - Sex Set 23, 2011 21:41
zig escreveu:![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Rpz, o negócio é o seguinte:
Quando você tem uma potência negativa, tu deve inverter a base dela. Por exemplo:

Então pense o seguinte: a fração geratriz de 0,05 é

, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
Veja:
![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
A raiz quadrada de vinte, você acha fácil, né?
Espero ter ajudado.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:23
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:24
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


 é uma função impar integrável em um intervalo fechado cujos os extremos do intervalo são números simétricos , então a integral de f sobre este intervalo vale zero .
é uma função impar integrável em um intervalo fechado cujos os extremos do intervalo são números simétricos , então a integral de f sobre este intervalo vale zero . ![[-3,3] [-3,3]](/latexrender/pictures/083d33f8040330c3051e16ce69a5b0df.png) e portanto integrável sobre este intervalo .Graças a proposição acima , o integral sobre
e portanto integrável sobre este intervalo .Graças a proposição acima , o integral sobre 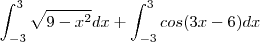 .
.
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.