 por KleinIll » Seg Mai 05, 2014 15:53
por KleinIll » Seg Mai 05, 2014 15:53
Q) Calcular o trabalho realizado pela força constante: f= 1i - 1j
para deslocar uma partícula ao longo da reta x+y=2 de A(0,2) até B(2,0)
R)
x(t) = t
y(t) = 2 - t
r(t) = (x(t), y(t))
r(t) = (t, 2 - t)


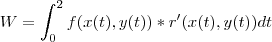
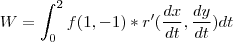
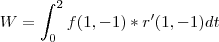



Está correta a solução?
??? ?? ? ????, ? ? ??????.
-

KleinIll
- Usuário Dedicado

-
- Mensagens: 46
- Registrado em: Qua Out 31, 2012 14:17
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Engenharia Química
- Andamento: formado
 por Russman » Seg Mai 05, 2014 18:40
por Russman » Seg Mai 05, 2014 18:40
Sim.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por KleinIll » Ter Mai 06, 2014 00:35
por KleinIll » Ter Mai 06, 2014 00:35
Russman escreveu:Sim.
Grato, Russman.
??? ?? ? ????, ? ? ??????.
-

KleinIll
- Usuário Dedicado

-
- Mensagens: 46
- Registrado em: Qua Out 31, 2012 14:17
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Engenharia Química
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Integral equivalente - Está correto?
por Cleyson007 » Qua Abr 18, 2012 16:07
- 1 Respostas
- 1574 Exibições
- Última mensagem por DanielFerreira

Qua Abr 18, 2012 20:54
Cálculo: Limites, Derivadas e Integrais
-
- Está correto? - Integral Iterada
 por Cleyson007 » Qua Abr 18, 2012 16:22
por Cleyson007 » Qua Abr 18, 2012 16:22
- 3 Respostas
- 1524 Exibições
- Última mensagem por DanielFerreira

Sáb Abr 21, 2012 17:31
Cálculo: Limites, Derivadas e Integrais
-
- [P.A.] Está correto?
por Cleyson007 » Dom Mai 25, 2008 19:37
- 1 Respostas
- 3154 Exibições
- Última mensagem por admin

Dom Mai 25, 2008 19:55
Progressões
-
- [determinante] Está correto?
por Cleyson007 » Sáb Jul 19, 2008 13:21
- 1 Respostas
- 3535 Exibições
- Última mensagem por admin

Sáb Jul 19, 2008 16:40
Matrizes e Determinantes
-
- [Derivada] Esta correto o que eu fiz?
por carvalhothg » Ter Set 13, 2011 13:22
- 2 Respostas
- 1856 Exibições
- Última mensagem por thiago toledo

Ter Set 13, 2011 18:21
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 10 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


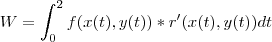
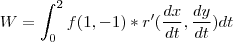
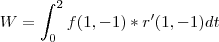






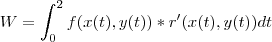
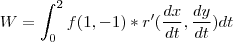
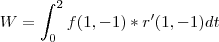






 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.