 por e8group » Sex Mai 02, 2014 14:04
por e8group » Sex Mai 02, 2014 14:04
Preciso limitar
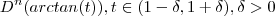
para determinar

de modo que o erro da aproximação de

por
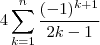
seja menor que

.
Alguém tem alguma ideia ? Como obter uma expressão para

?
Até agora só consegui isto abaixo ...
i) Primeiro vamos garantir que

é limitada em

.
Derivando
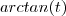
n-vezes , vamos obter uma expressão da forma

,onde

é um polinômio
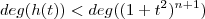
e portanto
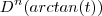
é uma função racional e

.Sendo assim garantimos que
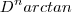
é contínua .Em particular , ela é contínua em qualquer intervalo fechado não degenerado contendo a vizinhança de

.Logo pelo Teorema de Weierstrass ,
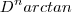
é limitada neste intervalo .
Assim ,

ii) Segunda parte trabalhosa, determinar

e encontrar uma cota .
Pensei assim :
Seja
![I_n (t) = D^n(arctan(t)) = D^n \left(\int_0^t \frac{d\zeta }{1+ \zeta^2}\right) = \frac{1}{2i}D^n \left(\int_0^t \left[ \frac{1 }{t -i} - \frac{1 }{t +i} \right ]d \zeta \right) I_n (t) = D^n(arctan(t)) = D^n \left(\int_0^t \frac{d\zeta }{1+ \zeta^2}\right) = \frac{1}{2i}D^n \left(\int_0^t \left[ \frac{1 }{t -i} - \frac{1 }{t +i} \right ]d \zeta \right)](/latexrender/pictures/d7c19ec5b41f47b62c610c156d7f5e04.png)
Daí , temos
![I_n(t) = \frac{1}{2i}(-1)^n n! \left[ \frac{1}{(t-i)^{n+1}} - \frac{1}{(t+i)^{n+1}}\right ] = \frac{i}{2}(-1)^{n+1} \frac{n!}{(t+1)^{n+1}}\left[ (t+i)^{n+1}- (t-i)^{n+1}\right] I_n(t) = \frac{1}{2i}(-1)^n n! \left[ \frac{1}{(t-i)^{n+1}} - \frac{1}{(t+i)^{n+1}}\right ] = \frac{i}{2}(-1)^{n+1} \frac{n!}{(t+1)^{n+1}}\left[ (t+i)^{n+1}- (t-i)^{n+1}\right]](/latexrender/pictures/6b7f2ca704f1991f83afbb2817ea8384.png)
e finalmente obtemos
![I_n(t) = \frac{(-1)^{n+1}n!}{2(1+t)^{n+1}} \sum_{m=0}^{n+1} \binom{n+1}{m}[1-(-1)^{m+1}]i^{k+1} \cdot t^{n+1 -k} I_n(t) = \frac{(-1)^{n+1}n!}{2(1+t)^{n+1}} \sum_{m=0}^{n+1} \binom{n+1}{m}[1-(-1)^{m+1}]i^{k+1} \cdot t^{n+1 -k}](/latexrender/pictures/45dcf87ee4c76edf4cbac4078fde283f.png)
.
Logo ,
![|I_n(t)| = \frac{n!}{2(1+t)^{n+1}} | \sum_{m=0}^{n+1} \binom{n+1}{m}[1+(-1)^{m+1}]i^{k+1} \cdot t^{n+1 -k}| \leq \frac{n!}{2(1+t)^{n+1}} \cdot \sum_{m=0}^{n+1} \binom{n+1}{m}|(1-(-1)^{m+1})i^{k+1}|t^{n+1-k} \leq \frac{n!}{2(1+t)^{n+1}} \cdot \sum_{m=0}^{n+1} \binom{n+1}{m} t^{n+1-k} = \frac{n!}{2(1+t)^{n+1}} \cdot (1+t)^{n+1} = \frac{n!}{2} |I_n(t)| = \frac{n!}{2(1+t)^{n+1}} | \sum_{m=0}^{n+1} \binom{n+1}{m}[1+(-1)^{m+1}]i^{k+1} \cdot t^{n+1 -k}| \leq \frac{n!}{2(1+t)^{n+1}} \cdot \sum_{m=0}^{n+1} \binom{n+1}{m}|(1-(-1)^{m+1})i^{k+1}|t^{n+1-k} \leq \frac{n!}{2(1+t)^{n+1}} \cdot \sum_{m=0}^{n+1} \binom{n+1}{m} t^{n+1-k} = \frac{n!}{2(1+t)^{n+1}} \cdot (1+t)^{n+1} = \frac{n!}{2}](/latexrender/pictures/0726c60a3f905901b0974c49e518fa79.png)
.
Portanto
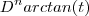
é limitada por
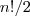
.
Mas esta cota não ajuda , meu objetivo era obter

.
iii) Encontrar

.
Sabemos que

(Forma Lagrange). , então

, .
Se tivéssemos demostrado que
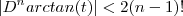
.
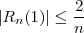
e com isso
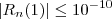
sempre que

que é a resposta do gabarito .
Qualquer ajuda é bem vinda .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [derivada]Erro de Aproximaçao
 por TheKyabu » Qua Out 31, 2012 10:10
por TheKyabu » Qua Out 31, 2012 10:10
- 1 Respostas
- 2236 Exibições
- Última mensagem por LuizAquino

Qui Nov 01, 2012 16:37
Cálculo: Limites, Derivadas e Integrais
-
- Estimativa
por brjohnsmith » Dom Jul 27, 2014 00:00
- 0 Respostas
- 2095 Exibições
- Última mensagem por brjohnsmith

Dom Jul 27, 2014 00:00
Aritmética
-
- Estimativa do modulo de x
por Roni Martins » Ter Mar 09, 2010 11:45
- 0 Respostas
- 1250 Exibições
- Última mensagem por Roni Martins

Ter Mar 09, 2010 11:45
Álgebra Elementar
-
- Estimativa de numeros reais
 por Roni Martins » Qui Fev 25, 2010 15:51
por Roni Martins » Qui Fev 25, 2010 15:51
- 1 Respostas
- 2335 Exibições
- Última mensagem por Molina

Qui Fev 25, 2010 18:30
Álgebra Elementar
-
- Aproximação
por Thais Aquino Lima » Qui Fev 28, 2013 19:28
- 1 Respostas
- 1319 Exibições
- Última mensagem por Cleyson007

Sex Mar 01, 2013 09:13
Aritmética
Usuários navegando neste fórum: Nenhum usuário registrado e 7 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
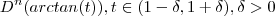 para determinar
para determinar  de modo que o erro da aproximação de
de modo que o erro da aproximação de  por
por 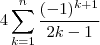 seja menor que
seja menor que  .
. ?
?  é limitada em
é limitada em  .
.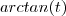 n-vezes , vamos obter uma expressão da forma
n-vezes , vamos obter uma expressão da forma  ,onde
,onde  é um polinômio
é um polinômio 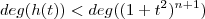 e portanto
e portanto 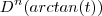 é uma função racional e
é uma função racional e  .Sendo assim garantimos que
.Sendo assim garantimos que 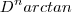 é contínua .Em particular , ela é contínua em qualquer intervalo fechado não degenerado contendo a vizinhança de
é contínua .Em particular , ela é contínua em qualquer intervalo fechado não degenerado contendo a vizinhança de  .Logo pelo Teorema de Weierstrass ,
.Logo pelo Teorema de Weierstrass , 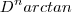 é limitada neste intervalo .
é limitada neste intervalo . 
 e encontrar uma cota .
e encontrar uma cota . ![I_n (t) = D^n(arctan(t)) = D^n \left(\int_0^t \frac{d\zeta }{1+ \zeta^2}\right) = \frac{1}{2i}D^n \left(\int_0^t \left[ \frac{1 }{t -i} - \frac{1 }{t +i} \right ]d \zeta \right) I_n (t) = D^n(arctan(t)) = D^n \left(\int_0^t \frac{d\zeta }{1+ \zeta^2}\right) = \frac{1}{2i}D^n \left(\int_0^t \left[ \frac{1 }{t -i} - \frac{1 }{t +i} \right ]d \zeta \right)](/latexrender/pictures/d7c19ec5b41f47b62c610c156d7f5e04.png)
![I_n(t) = \frac{1}{2i}(-1)^n n! \left[ \frac{1}{(t-i)^{n+1}} - \frac{1}{(t+i)^{n+1}}\right ] = \frac{i}{2}(-1)^{n+1} \frac{n!}{(t+1)^{n+1}}\left[ (t+i)^{n+1}- (t-i)^{n+1}\right] I_n(t) = \frac{1}{2i}(-1)^n n! \left[ \frac{1}{(t-i)^{n+1}} - \frac{1}{(t+i)^{n+1}}\right ] = \frac{i}{2}(-1)^{n+1} \frac{n!}{(t+1)^{n+1}}\left[ (t+i)^{n+1}- (t-i)^{n+1}\right]](/latexrender/pictures/6b7f2ca704f1991f83afbb2817ea8384.png) e finalmente obtemos
e finalmente obtemos ![I_n(t) = \frac{(-1)^{n+1}n!}{2(1+t)^{n+1}} \sum_{m=0}^{n+1} \binom{n+1}{m}[1-(-1)^{m+1}]i^{k+1} \cdot t^{n+1 -k} I_n(t) = \frac{(-1)^{n+1}n!}{2(1+t)^{n+1}} \sum_{m=0}^{n+1} \binom{n+1}{m}[1-(-1)^{m+1}]i^{k+1} \cdot t^{n+1 -k}](/latexrender/pictures/45dcf87ee4c76edf4cbac4078fde283f.png) .
. ![|I_n(t)| = \frac{n!}{2(1+t)^{n+1}} | \sum_{m=0}^{n+1} \binom{n+1}{m}[1+(-1)^{m+1}]i^{k+1} \cdot t^{n+1 -k}| \leq \frac{n!}{2(1+t)^{n+1}} \cdot \sum_{m=0}^{n+1} \binom{n+1}{m}|(1-(-1)^{m+1})i^{k+1}|t^{n+1-k} \leq \frac{n!}{2(1+t)^{n+1}} \cdot \sum_{m=0}^{n+1} \binom{n+1}{m} t^{n+1-k} = \frac{n!}{2(1+t)^{n+1}} \cdot (1+t)^{n+1} = \frac{n!}{2} |I_n(t)| = \frac{n!}{2(1+t)^{n+1}} | \sum_{m=0}^{n+1} \binom{n+1}{m}[1+(-1)^{m+1}]i^{k+1} \cdot t^{n+1 -k}| \leq \frac{n!}{2(1+t)^{n+1}} \cdot \sum_{m=0}^{n+1} \binom{n+1}{m}|(1-(-1)^{m+1})i^{k+1}|t^{n+1-k} \leq \frac{n!}{2(1+t)^{n+1}} \cdot \sum_{m=0}^{n+1} \binom{n+1}{m} t^{n+1-k} = \frac{n!}{2(1+t)^{n+1}} \cdot (1+t)^{n+1} = \frac{n!}{2}](/latexrender/pictures/0726c60a3f905901b0974c49e518fa79.png) .
. 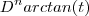 é limitada por
é limitada por 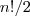 .
.  .
.  .
.  (Forma Lagrange). , então
(Forma Lagrange). , então  , .
, .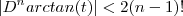 .
.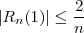 e com isso
e com isso 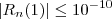 sempre que
sempre que  que é a resposta do gabarito .
que é a resposta do gabarito .






