Cálculo numérico, metodo de newton

[Crist]

tenho a funçao, f(x) = 3 cos(x) - e^(-0.4x), fiz o metodo gráfico e preciso da raiz negativa que está entre [-2,-1], isso foi a letra a do exercício.
agora na letra b não consigo a resoluçao correta, pelo metodo de newton, precisava escolher uma boa aproximaçao , escolhi x0= -1, e nao dá certo .E a derivada, achei: f´(x) = -3 sen(x) +0.4e^(-0.4x)
deu 3 iteraçoes
x3= -2,7581 o que tá longe de estar certo, socorro alguém me ajuda por favor
é para hoje até as 11:30 h

[young_jedi]

amigo utilizei a seguinte relação recursiva



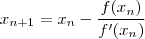
apos tres interações cheguei em -1,04087

[Crist]

usando x0 = -1?
tentei mas não dei conta , que tristeza, meu prazo acabou

[young_jedi]

foi utilizando x0=-1

voce utilizou equação de recorrencia corretamente?

[Crist]

usei, desde o inicio, mas é que era uma tarefa muito longa e cansativa e essa questão eu me perdi nos cálculos e com isso o prazo terminou, postei minha tarefa sem essa resolução, fiquei muito triste e frustrada comigo , pois eu entendi a matéria, sabia o processo mas não consegui chegar na resposta. Obrigada pela ajuda.