 por raimundoocjr » Sáb Out 19, 2013 20:38
por raimundoocjr » Sáb Out 19, 2013 20:38
Determine equações paramétricas da reta que é perpendicular ao plano 2x+4y+3z=0 e é também tangente à curva

(t)=(2t, t²-1, t²-t).
Comentário: "caiu" na minha prova de Cálculo 2.
Sei que pelo menos um vetor normal ao plano é formado pelos coeficientes das variáveis, então:
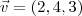
, e a derivada da curva é:
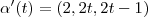
. A equação vetorial da reta é:
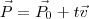
.
Nota: Equação do Plano:
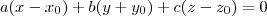
.
-
raimundoocjr
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Equações paramétricas da curva
por kalschne » Qui Fev 16, 2012 20:51
- 3 Respostas
- 2119 Exibições
- Última mensagem por kalschne

Qui Fev 16, 2012 22:48
Geometria Analítica
-
- [Equações Paramétricas] Comprimento da Curva
por vmouc » Ter Mar 27, 2012 14:53
- 3 Respostas
- 2368 Exibições
- Última mensagem por LuizAquino

Qui Abr 19, 2012 15:10
Cálculo: Limites, Derivadas e Integrais
-
- Equações cartesianas e equações paramétricas
por Victor Mello » Sáb Ago 23, 2014 16:24
- 1 Respostas
- 3435 Exibições
- Última mensagem por Russman

Sáb Ago 23, 2014 18:29
Funções
-
- Equaçoes parametricas
por angels900 » Ter Jan 31, 2012 14:35
- 6 Respostas
- 3740 Exibições
- Última mensagem por LuizAquino

Ter Jan 31, 2012 17:04
Geometria Analítica
-
- [Equações Paramétricas - Espaço]
por raimundoocjr » Ter Set 24, 2013 20:40
- 2 Respostas
- 1869 Exibições
- Última mensagem por raimundoocjr

Qua Set 25, 2013 19:05
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 (t)=(2t, t²-1, t²-t).
(t)=(2t, t²-1, t²-t).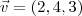 , e a derivada da curva é:
, e a derivada da curva é: 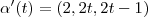 . A equação vetorial da reta é:
. A equação vetorial da reta é: 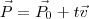 .
.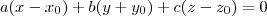 .
.