- A seguinte questão diz que um certo lago possui uma quantidade de rãs em um ano e quer saber a quantidade de rãs em 't' anos depois, com base em um modelo matemático de crescimento, sendo que o livro só da a derivada desse modelo de crescimento.
Enunciado na integra:
http://uploaddeimagens.com.br/imagens/enunciado-png
![\frac{d}{dt}\left[p(t)\right]={(3+0,12t)}^{\frac{3}{2}} \frac{d}{dt}\left[p(t)\right]={(3+0,12t)}^{\frac{3}{2}}](/latexrender/pictures/3b7fa3598000d8247a11bc9e128b8c74.png)
![\int_{}^{}\frac{d}{dt}\left[p(t)\right]dt=\int_{}^{}{(3+0,12t)}^{\frac{3}{2}}dt \int_{}^{}\frac{d}{dt}\left[p(t)\right]dt=\int_{}^{}{(3+0,12t)}^{\frac{3}{2}}dt](/latexrender/pictures/a460f856816381e47d69cb0f970e7d02.png)
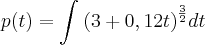


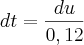
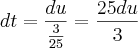

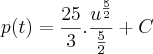

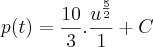
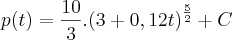
de 2005 a 2010 - 5 anos. t=5
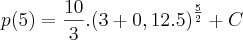
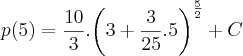
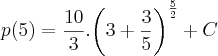

![p(5)=\frac{10}{3}.\sqrt[]{{\left(\frac{18}{5}\right)}^{5}}+C p(5)=\frac{10}{3}.\sqrt[]{{\left(\frac{18}{5}\right)}^{5}}+C](/latexrender/pictures/61faa0f5c1ce0c29bf01e6d5a0aff176.png)
![p(5)=\frac{10}{3}.\sqrt[]{{\left(\frac{18}{5}\right)}^{2}.{\left(\frac{18}{5}\right)}^{2}.\left(\frac{18}{5}\right)}+C p(5)=\frac{10}{3}.\sqrt[]{{\left(\frac{18}{5}\right)}^{2}.{\left(\frac{18}{5}\right)}^{2}.\left(\frac{18}{5}\right)}+C](/latexrender/pictures/4377d0f73553cc50829a299524c69fbc.png)
![p(5)=\frac{10}{3}.\frac{18}{5}.\frac{18}{5}\sqrt[]{\frac{18}{5}}+C p(5)=\frac{10}{3}.\frac{18}{5}.\frac{18}{5}\sqrt[]{\frac{18}{5}}+C](/latexrender/pictures/e57163560a55b4752b1fd48b642143fa.png)
![p(5)=\frac{2}{1}.\frac{6}{1}.\frac{18}{5}\sqrt[]{\frac{18}{5}}+C p(5)=\frac{2}{1}.\frac{6}{1}.\frac{18}{5}\sqrt[]{\frac{18}{5}}+C](/latexrender/pictures/bb4bd9d0bbd359809010c23ae87b8ab7.png)
![p(5)=\frac{216}{5}.\frac{\sqrt[]{18}}{\sqrt[]{5}}+C p(5)=\frac{216}{5}.\frac{\sqrt[]{18}}{\sqrt[]{5}}+C](/latexrender/pictures/4d177941549ce8d7ecaa3c9b96c43834.png)
![p(5)=\frac{216}{5}.\frac{3\sqrt[]{2}}{\sqrt[]{5}}+C p(5)=\frac{216}{5}.\frac{3\sqrt[]{2}}{\sqrt[]{5}}+C](/latexrender/pictures/838ce66453f4188933b8c3b92c4c5741.png)
![p(5)=\frac{648\sqrt[]{2}}{5\sqrt[]{5}}+C p(5)=\frac{648\sqrt[]{2}}{5\sqrt[]{5}}+C](/latexrender/pictures/a3c44b93865cb1179525f8a250c33abc.png)
- Bom.. Sabendo que no ponto '0', ou seja, no ano '0', que é o ano de 2005, há 100.000 rãs..


![100000=\frac{10}{3}.\sqrt[]{{3}^{5}}+C 100000=\frac{10}{3}.\sqrt[]{{3}^{5}}+C](/latexrender/pictures/7fa7d3a7e9b052a8861b9a0731823fb3.png)
![100000=\frac{10}{3}.\sqrt[]{{3}^{2}.{3}^{2}.3}+C 100000=\frac{10}{3}.\sqrt[]{{3}^{2}.{3}^{2}.3}+C](/latexrender/pictures/9aa7e5a036ad06198be361f09fab78db.png)
![100000=\frac{10}{3}.3.3\sqrt[]{3}+C 100000=\frac{10}{3}.3.3\sqrt[]{3}+C](/latexrender/pictures/3fd367d1b5eb4f993ba8c7860c1d0288.png)
![100000=10.3\sqrt[]{3}+C 100000=10.3\sqrt[]{3}+C](/latexrender/pictures/a2475a9c33ebed0739a2e9daa15c34ac.png)
![100000=30\sqrt[]{3}+C 100000=30\sqrt[]{3}+C](/latexrender/pictures/a485e6e8774d7c0472e4409bc156eb77.png)
![C=100000-30\sqrt[]{3} C=100000-30\sqrt[]{3}](/latexrender/pictures/6cd7f3e1a2c670fdc079dfc687523d68.png)
- logo:
![p(5)=\frac{648\sqrt[]{2}}{5\sqrt[]{5}}+100000-30\sqrt[]{3} p(5)=\frac{648\sqrt[]{2}}{5\sqrt[]{5}}+100000-30\sqrt[]{3}](/latexrender/pictures/a901d7995f1a5fe0ea33a0796ab3358c.png)
- E agora???? Essa não pode ser a resposta, pode?



![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)