 por Justiceira » Sex Out 30, 2009 16:29
por Justiceira » Sex Out 30, 2009 16:29
Estou com a seguinte dificuldade meu prof esta "ensinando" integrada indefinida porem ele não explicou muita coisa não.
Fui pegar um livro e vi este tipo de integrada indefinida que ate então nos exercicios dele não tinha nenhuma parecida.
Como faria pra calcular isso:
![\int_\:(5x^4-3x^3+2x)\frac{1}{\sqrt[6]{x^5}}dx \int_\:(5x^4-3x^3+2x)\frac{1}{\sqrt[6]{x^5}}dx](/latexrender/pictures/68aa61bc686947ce55be83f3cb13d148.png)
Me ensinem se possivel...ou me passem o nome de um bom livro sobre o assunto!!!

-

Justiceira
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Dom Set 27, 2009 12:26
- Formação Escolar: ENSINO FUNDAMENTAL II
- Andamento: cursando
 por thadeu » Sáb Out 31, 2009 13:28
por thadeu » Sáb Out 31, 2009 13:28
Separe as integrais:
![\int \frac{5x^4\,dx}{\sqrt[6]{x^5}}-\,\int \frac{3x^3\,dx}{\sqrt[6]{x^5}}+\,\int \frac{2x\,dx}{\sqrt[6]{x^5}}\\5 \int\,x^{4-\frac{5}{6}}dx\,-3 \int x^{3-\frac{5}{6}}dx\,+2 \int\,x^{1-\frac{5}{6}}dx\\5\,\int x^{\frac{19}{6}}dx-3 \int\,x^{\frac{13}{6}}dx+2 \int\,x^{\frac{1}{6}}dx\\5 (\frac{x^{\frac{25}{6}}}{\frac{25}{6}})-3 (\frac{x^{\frac{19}{6}}}{\frac{19}{6}})+2 (\frac{x^{\frac{7}{6}}}{\frac{7}{6}}) \int \frac{5x^4\,dx}{\sqrt[6]{x^5}}-\,\int \frac{3x^3\,dx}{\sqrt[6]{x^5}}+\,\int \frac{2x\,dx}{\sqrt[6]{x^5}}\\5 \int\,x^{4-\frac{5}{6}}dx\,-3 \int x^{3-\frac{5}{6}}dx\,+2 \int\,x^{1-\frac{5}{6}}dx\\5\,\int x^{\frac{19}{6}}dx-3 \int\,x^{\frac{13}{6}}dx+2 \int\,x^{\frac{1}{6}}dx\\5 (\frac{x^{\frac{25}{6}}}{\frac{25}{6}})-3 (\frac{x^{\frac{19}{6}}}{\frac{19}{6}})+2 (\frac{x^{\frac{7}{6}}}{\frac{7}{6}})](/latexrender/pictures/2cb08eabbed64c9afc00635bb485f3e4.png)
![\frac{6\,\sqrt[6]{x^{25}}}{5}\,-\,\frac{18\,\sqrt[6]{x^{19}}}{19}\,+\,\frac{12\,\sqrt[6]{x^7}}{7}\,+\,c \frac{6\,\sqrt[6]{x^{25}}}{5}\,-\,\frac{18\,\sqrt[6]{x^{19}}}{19}\,+\,\frac{12\,\sqrt[6]{x^7}}{7}\,+\,c](/latexrender/pictures/569dfa9e7ff5f3a407f5250840e13019.png)
Simplificando:
![\sqrt[6]{x}\,(\frac{6x^4}{5}\,-\,\frac{18x^3}{19}\,+\,\frac{12x}{7}) \sqrt[6]{x}\,(\frac{6x^4}{5}\,-\,\frac{18x^3}{19}\,+\,\frac{12x}{7})](/latexrender/pictures/72a55f926517eba7feb3044591ecc528.png)
Repare que eu apenas separei as integrais e simplifiquei seus expoentes; depois apenas usei
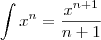
.
Espero ter ajudado!!!
-
thadeu
- Usuário Parceiro

-
- Mensagens: 69
- Registrado em: Seg Out 19, 2009 14:05
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Como aprender e entender matemática
por Bielto » Sáb Jul 14, 2012 13:55
- 8 Respostas
- 5698 Exibições
- Última mensagem por LuizAquino

Dom Jul 15, 2012 13:18
Álgebra Elementar
-
- Preciso entender como deu esse resultado!
por Adrielly » Qui Fev 11, 2010 11:26
- 4 Respostas
- 2346 Exibições
- Última mensagem por rojantsch

Sex Fev 19, 2010 12:56
Álgebra Elementar
-
- Entender como resolver média, a mediana e a moda
 por victorino29 » Ter Out 06, 2020 18:13
por victorino29 » Ter Out 06, 2020 18:13
- 2 Respostas
- 3935 Exibições
- Última mensagem por DanielFerreira

Seg Out 12, 2020 22:32
Estatística
-
- ME AJUDEM URGENTE PESSOAL
por Claudia Sotero » Seg Nov 23, 2009 22:15
- 1 Respostas
- 3400 Exibições
- Última mensagem por Neperiano

Sex Set 23, 2011 19:29
Funções
-
- [SEI N ] Pessoal Me ajudem Por favor!
por GarotoBurro » Sáb Mai 12, 2012 23:57
- 1 Respostas
- 1447 Exibições
- Última mensagem por DanielFerreira

Sáb Mai 19, 2012 10:29
Trigonometria
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Simplifique a expressão com radicais duplos
Autor:
Balanar - Seg Ago 09, 2010 04:01
Simplifique a expressão com radicais duplos abaixo:
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
Resposta:
Dica:
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
(dica : igualar a expressão a

e elevar ao quadrado os dois lados)
Assunto:
Simplifique a expressão com radicais duplos
Autor:
MarceloFantini - Qua Ago 11, 2010 05:46
É só fazer a dica.
Assunto:
Simplifique a expressão com radicais duplos
Autor:
Soprano - Sex Mar 04, 2016 09:49
Olá,
O resultado é igual a 1, certo?
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\int_\:(5x^4-3x^3+2x)\frac{1}{\sqrt[6]{x^5}}dx \int_\:(5x^4-3x^3+2x)\frac{1}{\sqrt[6]{x^5}}dx](/latexrender/pictures/68aa61bc686947ce55be83f3cb13d148.png)


![\int_\:(5x^4-3x^3+2x)\frac{1}{\sqrt[6]{x^5}}dx \int_\:(5x^4-3x^3+2x)\frac{1}{\sqrt[6]{x^5}}dx](/latexrender/pictures/68aa61bc686947ce55be83f3cb13d148.png)


![\int \frac{5x^4\,dx}{\sqrt[6]{x^5}}-\,\int \frac{3x^3\,dx}{\sqrt[6]{x^5}}+\,\int \frac{2x\,dx}{\sqrt[6]{x^5}}\\5 \int\,x^{4-\frac{5}{6}}dx\,-3 \int x^{3-\frac{5}{6}}dx\,+2 \int\,x^{1-\frac{5}{6}}dx\\5\,\int x^{\frac{19}{6}}dx-3 \int\,x^{\frac{13}{6}}dx+2 \int\,x^{\frac{1}{6}}dx\\5 (\frac{x^{\frac{25}{6}}}{\frac{25}{6}})-3 (\frac{x^{\frac{19}{6}}}{\frac{19}{6}})+2 (\frac{x^{\frac{7}{6}}}{\frac{7}{6}}) \int \frac{5x^4\,dx}{\sqrt[6]{x^5}}-\,\int \frac{3x^3\,dx}{\sqrt[6]{x^5}}+\,\int \frac{2x\,dx}{\sqrt[6]{x^5}}\\5 \int\,x^{4-\frac{5}{6}}dx\,-3 \int x^{3-\frac{5}{6}}dx\,+2 \int\,x^{1-\frac{5}{6}}dx\\5\,\int x^{\frac{19}{6}}dx-3 \int\,x^{\frac{13}{6}}dx+2 \int\,x^{\frac{1}{6}}dx\\5 (\frac{x^{\frac{25}{6}}}{\frac{25}{6}})-3 (\frac{x^{\frac{19}{6}}}{\frac{19}{6}})+2 (\frac{x^{\frac{7}{6}}}{\frac{7}{6}})](/latexrender/pictures/2cb08eabbed64c9afc00635bb485f3e4.png)
![\frac{6\,\sqrt[6]{x^{25}}}{5}\,-\,\frac{18\,\sqrt[6]{x^{19}}}{19}\,+\,\frac{12\,\sqrt[6]{x^7}}{7}\,+\,c \frac{6\,\sqrt[6]{x^{25}}}{5}\,-\,\frac{18\,\sqrt[6]{x^{19}}}{19}\,+\,\frac{12\,\sqrt[6]{x^7}}{7}\,+\,c](/latexrender/pictures/569dfa9e7ff5f3a407f5250840e13019.png)
![\sqrt[6]{x}\,(\frac{6x^4}{5}\,-\,\frac{18x^3}{19}\,+\,\frac{12x}{7}) \sqrt[6]{x}\,(\frac{6x^4}{5}\,-\,\frac{18x^3}{19}\,+\,\frac{12x}{7})](/latexrender/pictures/72a55f926517eba7feb3044591ecc528.png)
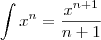 .
.


![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)