 por VenomForm » Seg Mai 20, 2013 13:29
por VenomForm » Seg Mai 20, 2013 13:29
Bom dia,
estou com duvida na seguinte função na qual tenho que calcular o seu comprimento de arco:
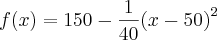
;
![\left[0,80 \right] \left[0,80 \right]](/latexrender/pictures/a3e6cc9c70053e4974b02e2c7d932721.png)
sei que a formula para calcular o comprimento de um arco é:
![\int_{a}^{b}\sqrt[2]{{f'(x)}^{2}+1}dx \int_{a}^{b}\sqrt[2]{{f'(x)}^{2}+1}dx](/latexrender/pictures/491b4c3bf37afa6052182900886a0bef.png)
então primeiro eu calculo a f'(x) que da:
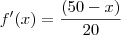
depois faço (f'(x))^2:

substituindo na formula:
![\int_{0}^{80}\sqrt[2]{\frac{{(50-x)}^{2}}{400}+1}dx \int_{0}^{80}\sqrt[2]{\frac{{(50-x)}^{2}}{400}+1}dx](/latexrender/pictures/6fc436ebf82ba5f377f3962f4b35a415.png)
Agora vem minha duvida, devo primeiro fazer alguma substituição para continuar a integração?se sim qual?
agradeço desde já pela sua ajuda
-
VenomForm
- Usuário Ativo

-
- Mensagens: 14
- Registrado em: Qua Fev 27, 2013 14:25
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Bacharelado em Ciências da Computação
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- comprimento do arco
por liviabgomes » Seg Mai 30, 2011 16:11
- 10 Respostas
- 6213 Exibições
- Última mensagem por liviabgomes

Qua Jun 01, 2011 15:03
Cálculo: Limites, Derivadas e Integrais
-
- comprimento de arco
por manuoliveira » Ter Out 23, 2012 19:43
- 0 Respostas
- 1309 Exibições
- Última mensagem por manuoliveira

Ter Out 23, 2012 19:43
Cálculo: Limites, Derivadas e Integrais
-
- Calculo do comprimento do arco.
por brunojorge29 » Seg Abr 23, 2012 11:21
- 3 Respostas
- 2951 Exibições
- Última mensagem por Russman

Seg Abr 23, 2012 22:32
Cálculo: Limites, Derivadas e Integrais
-
- Comprimento do arco!! Urgente!!
por manuoliveira » Ter Out 23, 2012 20:34
- 4 Respostas
- 3486 Exibições
- Última mensagem por manuoliveira

Ter Out 23, 2012 21:43
Cálculo: Limites, Derivadas e Integrais
-
- [Integral] Comprimento de Arco
por klueger » Qui Mar 21, 2013 10:19
- 5 Respostas
- 3390 Exibições
- Última mensagem por Russman

Qui Mar 21, 2013 12:54
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 10:38
Olá ! Tenho essa dúvida e não consigo montar o problema para resolução:
Qual é o racional não nulo cujo o quadrado é igual à sua terça parte ?
Grata.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 12:27

Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 12:55
também pensei que fosse assim, mas a resposta é

.
Obrigada Fantini.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 13:01

Como

:

O que você fez?
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 16:17
eu só consegui fazer a igualdade, não consegui desenvolver o restante, não pensei em fatoração, mas agora entendi o que vc fez.
Obrigada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
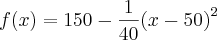 ;
;![\left[0,80 \right] \left[0,80 \right]](/latexrender/pictures/a3e6cc9c70053e4974b02e2c7d932721.png)
![\int_{a}^{b}\sqrt[2]{{f'(x)}^{2}+1}dx \int_{a}^{b}\sqrt[2]{{f'(x)}^{2}+1}dx](/latexrender/pictures/491b4c3bf37afa6052182900886a0bef.png)
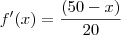

![\int_{0}^{80}\sqrt[2]{\frac{{(50-x)}^{2}}{400}+1}dx \int_{0}^{80}\sqrt[2]{\frac{{(50-x)}^{2}}{400}+1}dx](/latexrender/pictures/6fc436ebf82ba5f377f3962f4b35a415.png)



 .
.
 :
: