 por giboia90 » Seg Abr 29, 2013 14:57
por giboia90 » Seg Abr 29, 2013 14:57
é uma pergunta em inglês so queria uma explicação do resultado?
the points where the function f(x)= [x] + |1 -x|, -1<=x<=3, where [.] denotes the greatest integer function, is not differentiable, are:
resolução;
![f(x)= \left[x \right]+\left|1 -x \right| f(x)= \left[x \right]+\left|1 -x \right|](/latexrender/pictures/8bdd9ca74d806c44fa118b5c768cc948.png)
.......,


...................


...................


...................
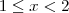

...................


...................

the only doubtful points are x = -1, 0, 1, 2, and 3. It can be easily seen that f(x) is differentiable at x= -1 but not differentiable at x = 0, 1, 2, and 3.
-
giboia90
- Usuário Dedicado

-
- Mensagens: 32
- Registrado em: Dom Dez 04, 2011 01:06
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engeharia civil
- Andamento: cursando
 por e8group » Seg Abr 29, 2013 15:57
por e8group » Seg Abr 29, 2013 15:57
Por definição ,

.
Assim ,podemos definir :
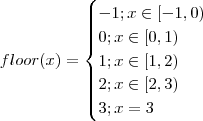
.
Retirando o módulo via definição ,temos :

.
Para verificar a continuidade ,basta calcular os limites (laterais) de cada extremo de cada intervalo .Lembrando que uma função é contínua sse

.Nos pontos em que a função é descontínua,pelo Lemma "Derivabilidade implica continuidade " podemos descartar a possibilidade da diferenciabilidade nestes pontos .Mas cuidado !! O recíproco deste Lemma não é verdadeiro .Nos pontos em que

é contínua devemos calular a derivada via definição .
Tente concluirf ...
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por giboia90 » Seg Abr 29, 2013 17:29
por giboia90 » Seg Abr 29, 2013 17:29
tem como fazer parte a parte de modo mais detalhado?
-
giboia90
- Usuário Dedicado

-
- Mensagens: 32
- Registrado em: Dom Dez 04, 2011 01:06
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engeharia civil
- Andamento: cursando
 por e8group » Seg Abr 29, 2013 18:49
por e8group » Seg Abr 29, 2013 18:49
Só por curiosidade ,já tentou esboçar o gráfico da função ? Este processo já fornece ideias de onde a função é descontínua , por conseguinte ,ela não será diferenciável nestes pontos .Vamos estudar a continuidade da função com respeito aos pontos
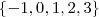
.
Considere :
i)

é contínua em

.
ii)
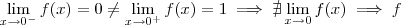
não é contínua em 0 .
OBS_1.: A função é descontínua também p/

,o argumento é semelhante .Deixo como exercício p/ tentar concluir .
Obs_2: Como diferenciabilidade implica continuidade já podemos afirmar que

não é derivável em tex] \{-0,1,2,3\}[/tex]
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![f(x)= \left[x \right]+\left|1 -x \right| f(x)= \left[x \right]+\left|1 -x \right|](/latexrender/pictures/8bdd9ca74d806c44fa118b5c768cc948.png) .......,
......., 
 ...................
...................
 ...................
...................
 ...................
...................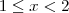
 ...................
...................
 ...................
...................


 .
. 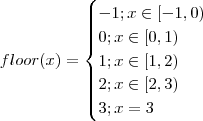 .
.  .
.  .Nos pontos em que a função é descontínua,pelo Lemma "Derivabilidade implica continuidade " podemos descartar a possibilidade da diferenciabilidade nestes pontos .Mas cuidado !! O recíproco deste Lemma não é verdadeiro .Nos pontos em que
.Nos pontos em que a função é descontínua,pelo Lemma "Derivabilidade implica continuidade " podemos descartar a possibilidade da diferenciabilidade nestes pontos .Mas cuidado !! O recíproco deste Lemma não é verdadeiro .Nos pontos em que  é contínua devemos calular a derivada via definição .
é contínua devemos calular a derivada via definição . 
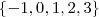 .
.  é contínua em
é contínua em  .
. 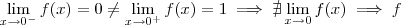 não é contínua em 0 .
não é contínua em 0 .  ,o argumento é semelhante .Deixo como exercício p/ tentar concluir .
,o argumento é semelhante .Deixo como exercício p/ tentar concluir .  .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  .
.
