 por Victor Gabriel » Qui Abr 18, 2013 13:24
por Victor Gabriel » Qui Abr 18, 2013 13:24
Suponha f integrável em

,para todo

. Prove que se
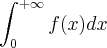
também é convergente. ( Sugestão:use que
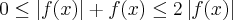
e que

.
Tem alguém que pode mim ajuda na resolução desta questão, pois não sei nem por onde começa!
-
Victor Gabriel
- Usuário Dedicado

-
- Mensagens: 48
- Registrado em: Dom Abr 14, 2013 20:29
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: estudante
- Andamento: cursando
 por Victor Gabriel » Dom Abr 21, 2013 12:03
por Victor Gabriel » Dom Abr 21, 2013 12:03
Victor Gabriel escreveu:Suponha f integrável em

,para todo

. Prove que se
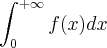
também é convergente. ( Sugestão:use que
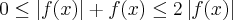
e que

.
Tem alguém que pode mim ajuda na resolução desta questão, pois não sei nem por onde começa!
e pessoal tem como alguém mim ajudar nesta questão?
-
Victor Gabriel
- Usuário Dedicado

-
- Mensagens: 48
- Registrado em: Dom Abr 14, 2013 20:29
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: estudante
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Converge ou diverge a sequencia
por Buda » Seg Out 24, 2011 21:28
- 11 Respostas
- 17072 Exibições
- Última mensagem por LuizAquino

Qua Nov 02, 2011 11:15
Sequências
-
- Série converge ou diverge
por Crist » Seg Fev 25, 2013 21:51
- 2 Respostas
- 2366 Exibições
- Última mensagem por Crist

Sáb Mar 02, 2013 10:16
Sequências
-
- Integral: converge
por Victor Gabriel » Seg Abr 29, 2013 14:57
- 0 Respostas
- 873 Exibições
- Última mensagem por Victor Gabriel

Seg Abr 29, 2013 14:57
Cálculo: Limites, Derivadas e Integrais
-
- [Integral] Estou com dificuldade para resolver esta integral
por Paulo Perez » Qui Out 03, 2013 12:22
- 2 Respostas
- 4611 Exibições
- Última mensagem por Paulo Perez

Sex Out 04, 2013 16:32
Cálculo: Limites, Derivadas e Integrais
-
- [INTEGRAL] Integral por partes! Alguem pode me ajudar?
por mih123 » Qua Jan 16, 2013 20:18
- 3 Respostas
- 4581 Exibições
- Última mensagem por adauto martins

Qua Out 22, 2014 09:11
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 7 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 ,para todo
,para todo  . Prove que se
. Prove que se 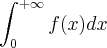 também é convergente. ( Sugestão:use que
também é convergente. ( Sugestão:use que 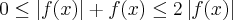 e que
e que  .
.
 ,para todo
,para todo  . Prove que se
. Prove que se 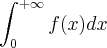 também é convergente. ( Sugestão:use que
também é convergente. ( Sugestão:use que 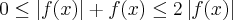 e que
e que  .
.
,para todo
. Prove que se
também é convergente. ( Sugestão:use que
e que
.






