 por walterdavid » Qui Out 01, 2009 21:21
por walterdavid » Qui Out 01, 2009 21:21
Boa noite pessoal. Estou com dúvida em algumas questões se puderem me ajudar seria ótimo.
1.resolver pelo teorema fundamental do cálculo

no meus livros não constam resolução com módulo entao não sei nem como começar
2

dispensa e
3
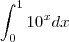
4: encontre os valores de c tal que a área da região limitada pelas parábolas

e

seja 576.
essa eu já tentei de tudo. mas esto com dificuldades pra enxergar a interseção formada e consequentemente os limites de integração. seria de -c á c? por que para descobrir os limites de int. em uma equação de área faz-se a interseção das equações certo?
agradeço a ajuda
Walter
-
walterdavid
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Qui Out 01, 2009 20:55
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Química
- Andamento: cursando
 por Lucio Carvalho » Sex Out 02, 2009 14:55
por Lucio Carvalho » Sex Out 02, 2009 14:55
Olá Walter,
Tentarei explicar os exercícios.
No 1º exercício, devemos lembrar que f(x) = |x + 1| =
-(x + 1) se x < -1
(x + 1) se x >= -1
Assim:


No 2º exercício, devemos lembrar por integração imediata que:
![\int_{}^{}\frac{f'(x)}{1+{f}^{2}(x)}dx=arctg[f(x)]+k \int_{}^{}\frac{f'(x)}{1+{f}^{2}(x)}dx=arctg[f(x)]+k](/latexrender/pictures/b5e4810fc3626b972228115f1f8ecb9a.png)
Assim:
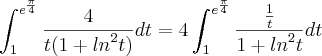
![\int_{1}^{{e}^{\frac{\pi}{4}}}\frac{4}{t(1+{ln}^{2}t)}dt=4.arctg[ln({e}^{\frac{\pi}{4}})]-4.arctg[ln(1)] \int_{1}^{{e}^{\frac{\pi}{4}}}\frac{4}{t(1+{ln}^{2}t)}dt=4.arctg[ln({e}^{\frac{\pi}{4}})]-4.arctg[ln(1)]](/latexrender/pictures/999b03402f9b815cbda4accf63acdba8.png)
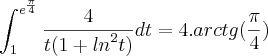
No terceiro exercício, sabemos por integração imediata que:
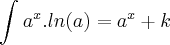
Assim:
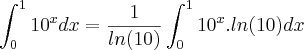
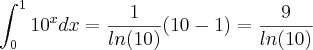
No 4º exercício, primeiro determinamos os limites de integração fazendo:

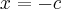
(limite inferior)

(limite superior)
Em seguida:
![\int_{-c}^{c}[({c}^{2}-{x}^{2})-({x}^{2}-{c}^{2})]dx=576 \int_{-c}^{c}[({c}^{2}-{x}^{2})-({x}^{2}-{c}^{2})]dx=576](/latexrender/pictures/a2ac0d8d98ae308f1a78f36b9adc1c40.png)


![c=\sqrt[3]{216}=6 c=\sqrt[3]{216}=6](/latexrender/pictures/6c2343e19cd73b0ffe9bb46acf7db278.png)
Espero ter ajudado e até breve!
-

Lucio Carvalho
- Colaborador Voluntário

-
- Mensagens: 127
- Registrado em: Qua Ago 19, 2009 11:33
- Localização: Rua 3 de Fevereiro - São Tomé
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Física/Química
- Andamento: formado
 por walterdavid » Ter Out 06, 2009 20:33
por walterdavid » Ter Out 06, 2009 20:33
nos cara ajudo demais da conta
muito obrigado mesmo
-
walterdavid
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Qui Out 01, 2009 20:55
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Química
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [integral] Volumes
por dehcalegari » Qui Ago 29, 2013 17:27
- 4 Respostas
- 2619 Exibições
- Última mensagem por dehcalegari

Sex Ago 30, 2013 11:49
Cálculo: Limites, Derivadas e Integrais
-
- Integral - áreas
por Danilo » Sáb Nov 09, 2013 18:42
- 1 Respostas
- 2127 Exibições
- Última mensagem por e8group

Sex Nov 15, 2013 11:44
Cálculo: Limites, Derivadas e Integrais
-
- Integral - Áreas
 por Danilo » Sex Nov 15, 2013 19:03
por Danilo » Sex Nov 15, 2013 19:03
- 2 Respostas
- 3523 Exibições
- Última mensagem por Man Utd

Qui Nov 21, 2013 17:20
Cálculo: Limites, Derivadas e Integrais
-
- Integral - Cálculo de áreas
por pinkfluor » Qui Jul 21, 2011 11:38
- 3 Respostas
- 2909 Exibições
- Última mensagem por pinkfluor

Qui Jul 21, 2011 17:21
Cálculo: Limites, Derivadas e Integrais
-
- Integral - Cálculo de áreas
 por AlbertoAM » Ter Jun 28, 2011 00:25
por AlbertoAM » Ter Jun 28, 2011 00:25
- 5 Respostas
- 6586 Exibições
- Última mensagem por AlbertoAM

Qua Jun 29, 2011 20:44
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


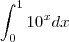
 e
e  seja 576.
seja 576.



![\int_{}^{}\frac{f'(x)}{1+{f}^{2}(x)}dx=arctg[f(x)]+k \int_{}^{}\frac{f'(x)}{1+{f}^{2}(x)}dx=arctg[f(x)]+k](/latexrender/pictures/b5e4810fc3626b972228115f1f8ecb9a.png)
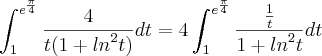
![\int_{1}^{{e}^{\frac{\pi}{4}}}\frac{4}{t(1+{ln}^{2}t)}dt=4.arctg[ln({e}^{\frac{\pi}{4}})]-4.arctg[ln(1)] \int_{1}^{{e}^{\frac{\pi}{4}}}\frac{4}{t(1+{ln}^{2}t)}dt=4.arctg[ln({e}^{\frac{\pi}{4}})]-4.arctg[ln(1)]](/latexrender/pictures/999b03402f9b815cbda4accf63acdba8.png)
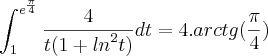
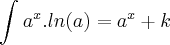
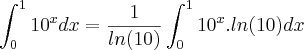
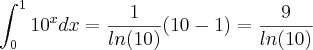

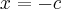 (limite inferior)
(limite inferior) (limite superior)
(limite superior)![\int_{-c}^{c}[({c}^{2}-{x}^{2})-({x}^{2}-{c}^{2})]dx=576 \int_{-c}^{c}[({c}^{2}-{x}^{2})-({x}^{2}-{c}^{2})]dx=576](/latexrender/pictures/a2ac0d8d98ae308f1a78f36b9adc1c40.png)


![c=\sqrt[3]{216}=6 c=\sqrt[3]{216}=6](/latexrender/pictures/6c2343e19cd73b0ffe9bb46acf7db278.png)

 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.