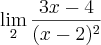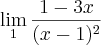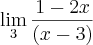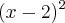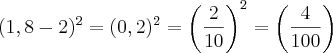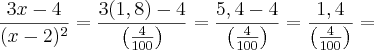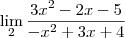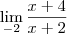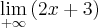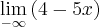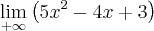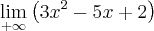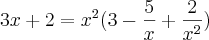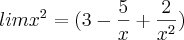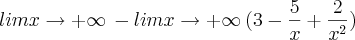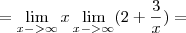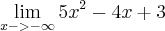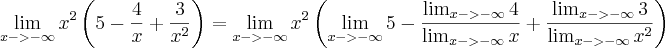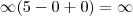por nakagumahissao » Qua Abr 10, 2013 16:04
por nakagumahissao » Qua Abr 10, 2013 16:04
Para o primeiro limite que corresponde a mais infinito, veja como você deverá vê-lo:
-------------------->--2--<-----------------------
Imagine uma reta como mostrada acima. O sinal '>' na reta indica que iremos tomar (pegar) valores bem próximos do dois vindo da esquerda. O sinal '<' indica que iremos tomar (pegar) valores bem próximos de dois, vindo da direita.
Agora, vindo da esquerda, imagine que peguemos um valor, digamos, x = 1,8. Isto significa que o denominador:
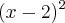
Será:
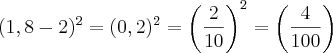
e a função toda ficará assim:
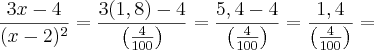

Tente agora fazer estas mesmas contas para x = 1,9, x=1,99, x = 1,9999 e você vai começar a perceber que o denominador será multiplicado por valores cada vez maiores que 100, ou seja, quanto mais nos aproximarmos de 2 pela esquerda da reta, o numerador aumentará cada vez mais, pois no limite, não estamos interessados em x = 2 e sim, em valores cada vez mais próximos de 2.
Tente também fazer estes mesmos cálculos vindo da direita de dois, ou seja, utilize x = 2,1, x= 2,01, x = 2,001, x = 2,0001 e você notará o mesmo comportamento.
Assim, conclui-se que este primeiro limite tende a 'mais infinito'.
Raciocine da mesma forma para o segundo limite apresentado e chegará a conclusão de que ele tende para 'menos infinito'
Para o terceiro, acredito que a resposta está errada. Não acredito que seja inexistente, e sim tende também à 'menos infinito'. Para que um limite não exista, os limites 'Laterais', ou seja, para este terceiro limite especificamente, o limite calculado quando se aproxima do valor 3 pela esquerda e o outro calculado quando o limite se aproxima do valor 3 pela direita deverão ser diferentes.
Espero ter ajudado.
Eu faço a diferença. E você?
Do Poema: Quanto os professores "fazem"?
De Taylor Mali
-
nakagumahissao
- Colaborador Voluntário

-
- Mensagens: 386
- Registrado em: Qua Abr 04, 2012 14:07
- Localização: Brazil
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Lic. Matemática
- Andamento: cursando
-
 por snoffao » Qui Abr 11, 2013 13:17
por snoffao » Qui Abr 11, 2013 13:17
Eu fiquei com uma duvida. Como eu irei saber por exemplo : ' nessa questao : vou fazer a substituição, a não agora vou usar a formula tal. ' Pra saber se é infinito ou inexistente Um exemplo :
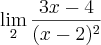
-> resultado = infinito positivo
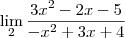
ps: TEM UM PARENTESES GRANDE NA FORMULA TODA E O EXPOENTE É 3
RESULTADO DESSA CONTA : 1/8
__
Todas abaixo o resultado é INEXISTENTE



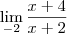
Entendeu minha duvida? Eu não estou conseguindo entender essa diferença . Como entender se ele é inexistente,+infinito e -infinito
OBS: Essas respostas foram dadas pelo professor .
-
snoffao
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Qua Abr 10, 2013 13:50
- Formação Escolar: GRADUAÇÃO
- Área/Curso: INFORMATICA
- Andamento: cursando
 por nakagumahissao » Qui Abr 11, 2013 13:32
por nakagumahissao » Qui Abr 11, 2013 13:32
snoffao,
Como foi dito já na primeira resposta:
O Limite Existe se os limites laterais existem e forem iguais. Se ao tender para um determinado valor os limites forem iguais e for crescendo indefinidamente, ele tende ao infinito. Por um outro lado, se os limites laterais forem iguais e o resultado do limite for decrescendo indefinidamente, dizemos que ele tende a 'menos' infinito. Se eles forem iguais e o resultado se aproximar de algum valor, o limite é igual à este valor. Se os limites laterais não forem iguais, ele não existe, ou seja é inexistente.
Caso tenha mais dúvidas a respeito de limites laterais, aconselho a dar uma revisada em algum livro de cálculo sobre o teorema da existência do limite por favor.
Espero que eu tenha conseguido explicar as diferenças entre 'tender' para valores (mesmo que sejam para mais ou menos infinito) e sua inexistência.
Eu faço a diferença. E você?
Do Poema: Quanto os professores "fazem"?
De Taylor Mali
-
nakagumahissao
- Colaborador Voluntário

-
- Mensagens: 386
- Registrado em: Qua Abr 04, 2012 14:07
- Localização: Brazil
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Lic. Matemática
- Andamento: cursando
-
 por snoffao » Qui Abr 11, 2013 16:30
por snoffao » Qui Abr 11, 2013 16:30
-
snoffao
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Qua Abr 10, 2013 13:50
- Formação Escolar: GRADUAÇÃO
- Área/Curso: INFORMATICA
- Andamento: cursando
 por nakagumahissao » Sex Abr 12, 2013 01:25
por nakagumahissao » Sex Abr 12, 2013 01:25
Eu faço a diferença. E você?
Do Poema: Quanto os professores "fazem"?
De Taylor Mali
-
nakagumahissao
- Colaborador Voluntário

-
- Mensagens: 386
- Registrado em: Qua Abr 04, 2012 14:07
- Localização: Brazil
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Lic. Matemática
- Andamento: cursando
-
 por snoffao » Dom Abr 14, 2013 11:49
por snoffao » Dom Abr 14, 2013 11:49
Obrigado, entendi mais ou menos.
Estou na duvida nessas questões aqui :
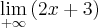
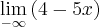
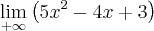


Resposta : + infinito , + infinito ,+ infinito ,-infinito , -infinito
Agora o infinito está no lugar do numero.
O professor deu esse exemplo aqui :
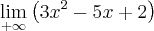
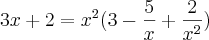
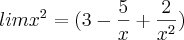
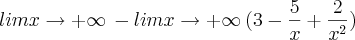

Tentei me guiar pra fazer os de cima nesse exercício mas não deu certo .
Tem como você me ajudar ?
Grato
-
snoffao
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Qua Abr 10, 2013 13:50
- Formação Escolar: GRADUAÇÃO
- Área/Curso: INFORMATICA
- Andamento: cursando
 por nakagumahissao » Dom Abr 14, 2013 13:32
por nakagumahissao » Dom Abr 14, 2013 13:32
Nesta primeira questão, colocamos primeiramente o x em evidência obtendo x(2 + 3/x).

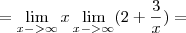

O que fazemos agora é intuitivo. Coloquei o meu pensamento no texto abaixo, mas na realidade esta conta que fazemos não pode ser feito como mostrado. Ele foi colocado somente para que você entenda o porque do resultado ficar +Infinito. O raciocínio é o seguinte:

Quando x tende ao infinito, o limite de também vai para o infinito. Imagine o gráfico de y = x. y é uma reta que passa na origem e vai para +Infinito, vindo de -Infinito à medida que x cresce não é mesmo? Então se y cresce à medida que x cresce indefinidamente, então y "caminha" para +infinito. Na segunda parte temos o limite de 2 quando x tende ao infinito. Neste caso, o gráfico de y = 2 é uma reta que passa em y=2 não importando o valor de x. Ou seja, para todo x, y sempre será dois. Então mesmo que x tenda ao infinito, y sempre será 2. Logo, o limite de 2 quando x tende ao infinito será 2! - Já a última parte, lembre-se que o limite do quociente é o quociente dos limites. Esta regra você já deve ter visto antes nas aulas de cálculo. Isto ocorre sempre que o limite do denominador (a parte de baixo da fração) seja diferente de zero. Ora, o limite do denominador (limite de x quando x tende ao infinito) é diferente de zero, pois x assume valores cada vez maiores), assim o limite de 3 quando x tende ao infinito é sempre 3 no numerador; no denominador o limite de x quando x tende ao infinito é um número cada vez maior. Logo, a divisão de 3 por um número cada vez maior leva este quociente para 0. Assim, Infinito multiplicado pela soma de 2 + 0 é igual a 2 multiplicado por infinito que dá infinito, que é a nossa resposta.
O segundo item:

é calculado de forma similar ao primeiro. Tente fazer você por favor. Aliás, procure resolver o máximo número de exercícios possível. Se eu resolver tudo o que colocou aqui, você não vai conseguir guardar estas informações. Procure por mais exercícios no livro ou na internet para praticar, isto vai lhe ajudar muito na assimilação do conteúdo.
O terceiro item:
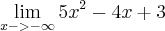
No que neste caso, podemos fatorar o polinômio da seguinte maneira:

Agora, calculando o limite:
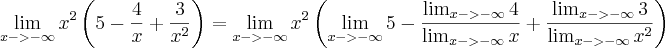
Ora, o Limite de x ao quadrado quando x tende a menos infinito é sempre +infinito (como está elevado ao quadrado, o resultado é sempre positivo); O limite de 5 quando x tende a menos infinito é sempre 5; O limite de 4 quando x tendo a menos infinito será sempre 4; Idem para o limite de 3 quando x tende a menos infinito; O Limite de x quando x tende a menos infinito, x tomará valores tão grandes e menor que zero que 4 dividido por um número negativo gigante fará com que a fração 4/x tenda para 0; Já o limite de x ao quadrado quando x tendo para menos infinito, assumirá valores POSITIVOS tão grandes quando x tende para menos infinito que a fração 3/x ficará 0 (ZERO).
LEMBRE-SE que podemos usar a propriedade do limite do quociente PORQUE x é diferente de zero na divisão! Se fosse zero, a propriedade do limite do quociente não poderia ser aplicada. (LEMBRANDO também que o LIMITE DO QUOCIENTE é o QUOCIENTE DOS LIMITES quando o limite do denominado for diferente de zero).
Assim:
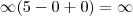
Os outros também são similares. Tente resolver você mesmo.
Espero ter ajudado.
Eu faço a diferença. E você?
Do Poema: Quanto os professores "fazem"?
De Taylor Mali
-
nakagumahissao
- Colaborador Voluntário

-
- Mensagens: 386
- Registrado em: Qua Abr 04, 2012 14:07
- Localização: Brazil
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Lic. Matemática
- Andamento: cursando
-
 por snoffao » Dom Abr 14, 2013 17:39
por snoffao » Dom Abr 14, 2013 17:39
Bela explicação .
Muito obrigado mesmo.
-
snoffao
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Qua Abr 10, 2013 13:50
- Formação Escolar: GRADUAÇÃO
- Área/Curso: INFORMATICA
- Andamento: cursando
 por snoffao » Dom Abr 14, 2013 17:39
por snoffao » Dom Abr 14, 2013 17:39
Bela explicação .
Muito obrigado mesmo.
-
snoffao
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Qua Abr 10, 2013 13:50
- Formação Escolar: GRADUAÇÃO
- Área/Curso: INFORMATICA
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Limite ao infinito] Dúvida na resposta = 0
por guilherme_vb » Ter Abr 23, 2013 11:27
- 1 Respostas
- 1433 Exibições
- Última mensagem por e8group

Sex Abr 26, 2013 22:10
Cálculo: Limites, Derivadas e Integrais
-
- [Limite ao Infinito] Duvida simples
por EduardoM » Ter Abr 23, 2013 17:25
- 2 Respostas
- 1521 Exibições
- Última mensagem por EduardoM

Sex Abr 26, 2013 19:52
Cálculo: Limites, Derivadas e Integrais
-
- duvida limite envolvendo simbo infinito.
por carlinhos23 » Seg Mai 30, 2011 03:40
- 2 Respostas
- 1550 Exibições
- Última mensagem por LuizAquino

Seg Mai 30, 2011 11:36
Cálculo: Limites, Derivadas e Integrais
-
- [limites no infinito]Limite no infinito de um ponto finito
por moyses » Ter Ago 30, 2011 12:45
- 3 Respostas
- 3528 Exibições
- Última mensagem por LuizAquino

Ter Ago 30, 2011 18:57
Cálculo: Limites, Derivadas e Integrais
-
- Dúvida Limite no infinito "m<n"
por elyjunior » Seg Set 26, 2011 22:59
- 2 Respostas
- 1821 Exibições
- Última mensagem por LuizAquino

Ter Set 27, 2011 17:09
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 7 visitantes
Assunto:
Proporcionalidade
Autor:
silvia fillet - Qui Out 13, 2011 22:46
Divida o numero 35 em partes diretamente proporcionais a 4, 10 e 14. Em seguida divida o mesmo numero em partes proporcionais a 6, 15 e 21. explique por que os resultados sao iguais.
Assunto:
Proporcionalidade
Autor:
silvia fillet - Sáb Out 15, 2011 10:25
POR GENTILEZA PODEM VERIFICAR SE O MEU RACIOCINIO ESTÁ CERTO?
P1 = K.4 SUBSTITUINDO K POR 1,25 P1= 5
P2 = K.10 SUBSTITUINDO K POR 1,25 P2= 12,50
P3 = K.13 SUBSTITUINDO K POR 1,25 P3= 17,50
P1+P2+P3 = 35
K.4+K.10+K.13 = 35
28 K = 35
K= 1,25
P1 = K.6 SUBSTITUINDO K POR 0,835 P1= 5
P2 = K.15 SUBSTITUINDO K POR 0,835 P2 = 12,50
P3 = K.21 SUBSTITUINDO K POR 0,835 P3 = 17,50
K.6+K.15+K.21 = 35
42K = 35
K= 0,833
4/6 =10/15 =14/21 RAZÃO = 2/3
SERÁ QUE ESTÁ CERTO?
ALGUEM PODE ME AJUDAR A EXPLICAR MELHOR?
OBRIGADA
SILVIA
Assunto:
Proporcionalidade
Autor:
ivanfx - Dom Out 16, 2011 00:37
utilize a definição e não se baseie no exercícios resolvidos da redefor, assim você terá mais clareza, mas acredito que sua conclusão esteja correto, pois o motivo de darem o mesmo resultado é pq a razão é a mesma.
Assunto:
Proporcionalidade
Autor:
Marcos Roberto - Dom Out 16, 2011 18:24
Silvia:
Acho que o resultado é o mesmo pq as razões dos coeficientes e as razões entre os números são inversamente proporcionais.
Você conseguiu achar o dia em que caiu 15 de novembro de 1889?
Assunto:
Proporcionalidade
Autor:
deiasp - Dom Out 16, 2011 23:45
Ola pessoal
Tb. estou no redefor
O dia da semana em 15 de novembro de 1889, acredito que foi em uma sexta feira
Assunto:
Proporcionalidade
Autor:
silvia fillet - Seg Out 17, 2011 06:23
Bom dia,
Realmente foi uma sexta feira, como fazer os calculos para chegar ?
Assunto:
Proporcionalidade
Autor:
ivanfx - Seg Out 17, 2011 07:18
Para encontrar o dia que caiu 15 de novembro de 1889 você deve em primeiro lugar encontrar a quantidade de anos bissextos que houve entre 1889 à 2011, após isso dá uma verificada no ano 1900, ele não é bissexto, pois a regra diz que ano que é múltiplo de 100 e não é múltiplo de 400 não é bissexto.
Depois calcule quantos dias dão de 1889 até 2011, basta pegar a quantidade de anos e multiplicar por 365 + 1 dia a cada ano bissexto (esse resultado você calculou quando encontrou a quantidade de anos bissextos)
Pegue o resultado e divida por 7 e vai obter o resto.
obtendo o resto e partindo da data que pegou como referência conte a quantidade do resto para trás da semana.
Assunto:
Proporcionalidade
Autor:
silvia fillet - Seg Out 17, 2011 07:40
Bom dia,
Será que é assim:
2011 a 1889 são 121 anos sendo , 30 anos bissextos e 91 anos normais então temos:
30x366 = 10.980 dias
91x365 = 33.215 dias
incluindo 15/11/1889 - 31/12/1889 47 dias
33215+10980+47 = 44242 dias
44242:7 = 6320 + resto 2
è assim, nâo sei mais sair disso.
Assunto:
Proporcionalidade
Autor:
ivanfx - Seg Out 17, 2011 10:24
que tal descontar 1 dia do seu resultado, pois 1900 não é bissexto, ai seria 44241 e quando fizer a divisão o resto será 1
como etá pegando base 1/01/2011, se reparar bem 01/01/2011 sempre cai no mesmo dia que 15/01/2011, sendo assim se 01/01/2011 caiu em um sábado volte 1 dia para trás, ou seja, você está no sábado e voltando 1 dia voltará para sexta.então 15/11/1889 cairá em uma sexta
Assunto:
Proporcionalidade
Autor:
Kiwamen2903 - Seg Out 17, 2011 19:43
Boa noite, sou novo por aqui, espero poder aprender e ajudar quando possível! A minha resposta ficou assim:
De 1889 até 2001 temos 29 anos bissextos a começar por 1892 (primeiro múltiplo de 4 após 1889) e terminar por 2008 (último múltiplo de 4 antes de 2011). Vale lembrar que o ano 1900 não é bissexto, uma vez que é múltiplo de 100 mas não é múltiplo de 400.
De um ano normal para outro, se considerarmos a mesma data, eles caem em dias consecutivos da semana. Por exemplo 01/01/2011 – sábado, e 01/01/2010 – sexta.
De um ano bissexto para outro, se considerarmos a mesma data, um cai dois dias da semana depois do outro. Por exemplo 01/01/2008 (ano bissexto) – Terça – feira, e 01/01/09 – Quinta-feira.
Sendo assim, se contarmos um dia da semana de diferença para cada um dos 01/01 dos 122 anos que separam 1889 e 2011 mais os 29 dias a mais referentes aos anos bissextos entre 1889 e 2011, concluímos que são 151 dias da semana de diferença, o que na realidade nos trás: 151:7= 21x7+4, isto é, são 4 dias da semana de diferença. Logo, como 15/11/2011 cairá em uma terça-feira, 15/11/1889 caiu em uma sexta-feira.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.