 por marcosmuscul » Qua Abr 03, 2013 19:09
por marcosmuscul » Qua Abr 03, 2013 19:09
consigo derivar.
consigo isolar x.
mas creio que não seja isso que pede-se.
preciso de ajuda.
- Anexos
-

-
marcosmuscul
- Usuário Dedicado

-
- Mensagens: 39
- Registrado em: Ter Mar 19, 2013 15:48
- Localização: RJ
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: a começar engenharia civil
- Andamento: cursando
 por e8group » Qua Abr 03, 2013 19:46
por e8group » Qua Abr 03, 2013 19:46
Considere uma equação nas variáveis

.Uma função

é dada implicitamente por tal equação se ,

, o ponto

satisfazer a equação .
A equação do segundo grau 2 em y (dada) tem solução em y :
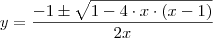
.
Assim , a função

é dada implicitamente pela equação
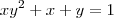
.
E ,é claro que a função

também é dada implicitamente pela equação
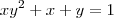
Observe que ambas funções estão bem definidas
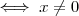
e

.
Tente concluir .
OBS.: Anexe imagens se for estritamente necessário ,neste caso não o é .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por marcosmuscul » Qua Abr 03, 2013 19:57
por marcosmuscul » Qua Abr 03, 2013 19:57
nesse caso voce utilizou a fórmula usada pra encontrar as raízes de uma equação de 2°grau. até aí entendi.
mas...e se fosse uma expressão em que aparecesse y³ ao invés de y²?
teríamos que saber de cabeça a fórmula de encontrar raízes de equações de 3°grau?
-
marcosmuscul
- Usuário Dedicado

-
- Mensagens: 39
- Registrado em: Ter Mar 19, 2013 15:48
- Localização: RJ
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: a começar engenharia civil
- Andamento: cursando
 por e8group » Qua Abr 03, 2013 20:26
por e8group » Qua Abr 03, 2013 20:26
Não necessariamente ,há equações do terceiro grau que facilmente conseguimos calcular uma de suas raízes,desta forma poderemos fatorar este polinômio .Se esta equação possui mais duas soluções é fácil obter elas através da fórmula resolvente da equação do segundo grau .
Exemplo :
A equação

possui uma única raiz que é

,pois

e

.
Já o próximo exemplo não é tão simples que é
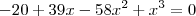
neste caso é útil recorrer a fórmula resolvente para equações de grau 3 .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Ajuda não entendi o enunciado] Limites
por elisafrombrazil » Sáb Jan 21, 2017 10:39
- 2 Respostas
- 5335 Exibições
- Última mensagem por e8group

Qua Fev 01, 2017 16:57
Cálculo: Limites, Derivadas e Integrais
-
- [Função]Não entendi
por Giudav » Sex Abr 13, 2012 00:30
- 1 Respostas
- 1425 Exibições
- Última mensagem por LuizAquino

Sáb Abr 14, 2012 12:20
Funções
-
- [continuidade de função]não entendi esse exemplo.
 por marcosmuscul » Ter Mar 26, 2013 19:52
por marcosmuscul » Ter Mar 26, 2013 19:52
- 0 Respostas
- 1288 Exibições
- Última mensagem por marcosmuscul

Ter Mar 26, 2013 19:52
Cálculo: Limites, Derivadas e Integrais
-
- [Função exponencial] Não entendi como chegou a formula
por Leti Moura » Ter Jun 12, 2012 21:16
- 2 Respostas
- 4088 Exibições
- Última mensagem por Russman

Qua Jun 13, 2012 00:57
Funções
-
- [Derivada] Função Implicita
por fabriel » Sex Mar 15, 2013 13:27
- 1 Respostas
- 1527 Exibições
- Última mensagem por e8group

Sex Mar 15, 2013 21:50
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 7 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



 .Uma função
.Uma função  é dada implicitamente por tal equação se ,
é dada implicitamente por tal equação se , , o ponto
, o ponto  satisfazer a equação .
satisfazer a equação .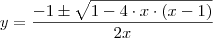 .
.  é dada implicitamente pela equação
é dada implicitamente pela equação 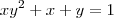 .
. também é dada implicitamente pela equação
também é dada implicitamente pela equação 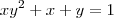
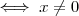 e
e  .
. 

 possui uma única raiz que é
possui uma única raiz que é  ,pois
,pois  e
e  .
.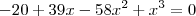 neste caso é útil recorrer a fórmula resolvente para equações de grau 3 .
neste caso é útil recorrer a fórmula resolvente para equações de grau 3 .

 .
.



