Não estou conseguindo nem a pau resolver esse limite... Eu fatorei a expressão de cima, mas a de baixo não consegui fatorar de jeito nenhum...
Como devo proceder?
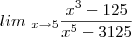

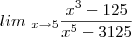

 e
e 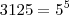 .
. 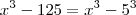 e
e 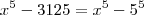 .
.  natural
natural 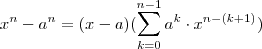 .
. 
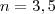 .
. 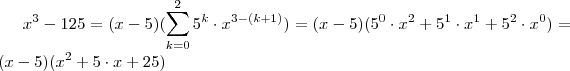
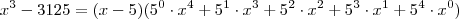 .
. 
santhiago escreveu:Vejae
.
Assim ,e
.
Em geral para qualquernatural
.
Fazendo
.
(a)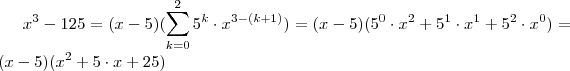
(b).
Tente concluir a parti daí .
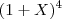 ?
?
 não podemos utilizar o mesmo método para fatorar ,pelo seguintes motivos ,primeiro a sua forma fatorada que é
não podemos utilizar o mesmo método para fatorar ,pelo seguintes motivos ,primeiro a sua forma fatorada que é  que difere da mesma apresentada no post anterior .Segundo ,
que difere da mesma apresentada no post anterior .Segundo , corresponde ao polinômio (obtido pelo Binômio de Newton )
corresponde ao polinômio (obtido pelo Binômio de Newton ) que não é da forma
que não é da forma  . Espero que não confundi você .
. Espero que não confundi você .  por
por  e analisar o comportamento verá a forma fatorada de
e analisar o comportamento verá a forma fatorada de  a qual eu mencionei utilizando o somatório para não ter que escrever todas aquelas parcelas .
a qual eu mencionei utilizando o somatório para não ter que escrever todas aquelas parcelas .
santhiago escreveu:No casonão podemos utilizar o mesmo método para fatorar ,pelo seguintes motivos ,primeiro a sua forma fatorada que é
que difere da mesma apresentada no post anterior .Segundo ,
corresponde ao polinômio (obtido pelo Binômio de Newton )
que não é da forma
. Espero que não confundi você .
Só para acrescentar , se você dividirpor
e analisar o comportamento verá a forma fatorada de
a qual eu mencionei utilizando o somatório para não ter que escrever todas aquelas parcelas .
É muito difícil avaliar se certa propriedade satisfaz um exerício satisfará outro,cada um possui suas particularidades e podem ter mais possibilidades de propriedades resolventes .Quando digo propriedade pode ser , "artifício " algébrico ,proposições,teoremas, e etc .

Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 5 visitantes
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
zig escreveu:

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.