 por Sobreira » Qua Mar 20, 2013 09:36
por Sobreira » Qua Mar 20, 2013 09:36
O exercício é o seguinte:
O vetor n é normal à curva de equação dada no ponto p.Determine n, nos casos:
a)
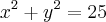
, p= (3,4),
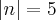
Eu calculei o vetor normal através do
f(p).
=

=
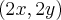
Substituindo 3 em x e 4 em y, então o vetor será n (6,8).
Mas a resposta é (3,4), eu sei que como foi especificado o módulo do vetor (5), e com (6,8) não dá módulo 5, a resposta não pode ser (6,8).
Como posso resolver então??
"The good thing about science is that it's true whether or not you believe in it."
-
Sobreira
- Colaborador Voluntário

-
- Mensagens: 122
- Registrado em: Sex Out 12, 2012 17:33
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: formado
 por nakagumahissao » Qua Mar 20, 2013 10:31
por nakagumahissao » Qua Mar 20, 2013 10:31
A idéia está correta ao meu ver, mas com perdão da palavra e somente para ilustrar, creio que melhor notação neste caso seria, ao invés de:
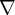
=

=
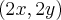
, ser

No ponto dado, ou seja, P=(3,4), teremos:
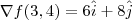
Até aqui, creio que não seja novidade. No entanto, como se trata de uma normal, o coeficiente angular seria 8/6 ou seja, 4/3. O que implica em dizer que (2x, 2y) = (x, y) = (3, 4) ao meu ver. Desta maneira, o módulo será de |9 + 16| = |25| = 5. Espero estar ajudando.
Eu faço a diferença. E você?
Do Poema: Quanto os professores "fazem"?
De Taylor Mali
-
nakagumahissao
- Colaborador Voluntário

-
- Mensagens: 386
- Registrado em: Qua Abr 04, 2012 14:07
- Localização: Brazil
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Lic. Matemática
- Andamento: cursando
-
 por Sobreira » Qua Mar 20, 2013 11:17
por Sobreira » Qua Mar 20, 2013 11:17
Cara obrigado pelas dicas com relação às notações.
Agora sinceramente continuo sem entender.Como disse sei que com (6,8) não vou conseguir um módulo igual a 5.Mas daí a ver com quais coordenadas do vetor eu consigo este valor de módulo é que está me dificultando.
Outro exemplo:
b)
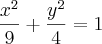
, ordenada de p igual a 0, abscissa de p positiva,
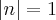
.
Substituindo 0 na ordenada, fico com:
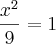
x=3, Então p(3,0)
Resolvendo as derivadas parciais em relação a x e y fica:

Substituindo p(3,0) ficaria

, mas aí acontece o mesmo caso de o modulo não dá "1", e a resposta desta questão é (1,0).
"The good thing about science is that it's true whether or not you believe in it."
-
Sobreira
- Colaborador Voluntário

-
- Mensagens: 122
- Registrado em: Sex Out 12, 2012 17:33
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: formado
 por Sobreira » Sex Mar 22, 2013 14:38
por Sobreira » Sex Mar 22, 2013 14:38
E aí pessoal?
Ninguém pode me ajudar??
Realmente não consegui resolver este exercício.
"The good thing about science is that it's true whether or not you believe in it."
-
Sobreira
- Colaborador Voluntário

-
- Mensagens: 122
- Registrado em: Sex Out 12, 2012 17:33
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Calcular reta tangente e normal à curva
por Kingflare » Dom Dez 07, 2014 23:54
- 1 Respostas
- 2690 Exibições
- Última mensagem por Molina

Qua Dez 17, 2014 14:15
Cálculo: Limites, Derivadas e Integrais
-
- Vetor normal a uma esfera
por suziquim » Sex Jul 01, 2011 13:03
- 0 Respostas
- 3084 Exibições
- Última mensagem por suziquim

Sex Jul 01, 2011 13:03
Geometria Analítica
-
- Como descobrir um vetor normal ao plano
por Thiago Silveira » Qua Jun 08, 2011 23:26
- 1 Respostas
- 41653 Exibições
- Última mensagem por LuizAquino

Qui Jun 09, 2011 23:18
Geometria Analítica
-
- calculo - pontos da curva
por caiofisico » Qui Out 27, 2011 13:12
- 8 Respostas
- 4379 Exibições
- Última mensagem por caiofisico

Sex Out 28, 2011 20:10
Cálculo: Limites, Derivadas e Integrais
-
- [Cálculo]classe da curva, significado
por Camolas » Sex Mai 31, 2013 14:51
- 0 Respostas
- 1219 Exibições
- Última mensagem por Camolas

Sex Mai 31, 2013 14:51
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 7 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
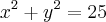 , p= (3,4),
, p= (3,4), 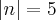
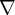 f(p).
f(p).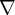 =
= =
= 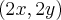



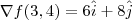
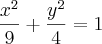 , ordenada de p igual a 0, abscissa de p positiva,
, ordenada de p igual a 0, abscissa de p positiva, 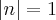 .
.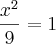

 , mas aí acontece o mesmo caso de o modulo não dá "1", e a resposta desta questão é (1,0).
, mas aí acontece o mesmo caso de o modulo não dá "1", e a resposta desta questão é (1,0).




