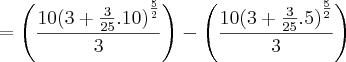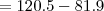por Matheus Lacombe O » Qui Mar 14, 2013 12:57
por Matheus Lacombe O » Qui Mar 14, 2013 12:57
-
Matheus Lacombe O
- Usuário Dedicado

-
- Mensagens: 36
- Registrado em: Sex Jun 03, 2011 22:37
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Eng. Mecânica
- Andamento: cursando
 por Russman » Qui Mar 14, 2013 14:08
por Russman » Qui Mar 14, 2013 14:08
O tempo é medido na função em "após t anos". Assim, como do início de 2005 até o inicio de 2010 passaram-se 5 anos, você deve fazer a integral de t=0 até t=5 e não de t=5 até t=10.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Crescimento de uma população de rãs com integral.
por Matheus Lacombe O » Dom Ago 04, 2013 18:26
- 3 Respostas
- 2000 Exibições
- Última mensagem por Russman

Ter Ago 06, 2013 13:59
Cálculo: Limites, Derivadas e Integrais
-
- Integral indefinida
por gdarius » Ter Mar 16, 2010 15:57
- 5 Respostas
- 5635 Exibições
- Última mensagem por DanielFerreira

Sáb Mar 31, 2012 19:32
Cálculo: Limites, Derivadas e Integrais
-
- Integral indefinida
 por CrazzyVi » Ter Ago 17, 2010 21:41
por CrazzyVi » Ter Ago 17, 2010 21:41
- 1 Respostas
- 2713 Exibições
- Última mensagem por Lucio Carvalho

Qua Ago 18, 2010 08:27
Cálculo: Limites, Derivadas e Integrais
-
- Integral indefinida
por felipealves » Ter Jun 21, 2011 11:48
- 3 Respostas
- 3992 Exibições
- Última mensagem por felipealves

Ter Jun 21, 2011 20:59
Cálculo: Limites, Derivadas e Integrais
-
- [Integral] indefinida
por Aliocha Karamazov » Qui Mar 01, 2012 20:30
- 7 Respostas
- 5056 Exibições
- Última mensagem por Aliocha Karamazov

Sáb Mar 03, 2012 21:59
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.

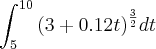

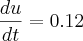


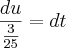

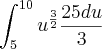
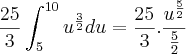
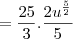

![\frac{25}{3}\int_{5}^{10}{u^{\frac{3}{2}}du=\left[\frac{10{u}^{\frac{5}{2}}}{3}{{\right]}_{5}}^{10} \frac{25}{3}\int_{5}^{10}{u^{\frac{3}{2}}du=\left[\frac{10{u}^{\frac{5}{2}}}{3}{{\right]}_{5}}^{10}](/latexrender/pictures/d02cf9a6722c6c790492ccc58d2d38b3.png)
![\frac{25}{3}\int_{5}^{10}{(3+0.12t)}^{\frac{3}{2}}dt=\left[\frac{10{(3+0.12t)}^{\frac{5}{2}}}{3}{{\right]}_{5}}^{10} \frac{25}{3}\int_{5}^{10}{(3+0.12t)}^{\frac{3}{2}}dt=\left[\frac{10{(3+0.12t)}^{\frac{5}{2}}}{3}{{\right]}_{5}}^{10}](/latexrender/pictures/9a42f7b43ff8494bc2a07f8d7f2755f6.png)