 por Matheus Lacombe O » Sáb Mar 02, 2013 23:54
por Matheus Lacombe O » Sáb Mar 02, 2013 23:54
- Olá pessoal! Cá estou eu, mais uma vez. Pois bem. Tenho uma lista com setenta exercícios do livro
Calculo(Howard Anton) para resolver. Resolvi sem problema os primeiros exercícios, porém, chegando ao nº6 encontrei uma dificuldade que parece ser comum a todos os itens deste exercício: depois de aplicar a substituição eu termino com uma expressão onde não consigo mais integrar, pois não é possível "trazer o denominador para cima".
nº6) Item c)
![\int_{}^{}\frac{1}{x\sqrt[]{9{x}^{2}-1}}dx \int_{}^{}\frac{1}{x\sqrt[]{9{x}^{2}-1}}dx](/latexrender/pictures/c1118fa067dab539f80f68636b31fa7f.png)
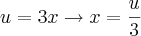


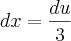
![\int_{}^{}\frac{1}{\frac{u\sqrt[]{{u}^{2}-1}}{3}}.\frac{du}{3} \int_{}^{}\frac{1}{\frac{u\sqrt[]{{u}^{2}-1}}{3}}.\frac{du}{3}](/latexrender/pictures/0dc0be322fd299ad9c298f433fc3dc80.png)
![\int_{}^{}\frac{1}{1}.\frac{3}{u\sqrt[]{{u}^{2}-1}}.\frac{du}{3} \int_{}^{}\frac{1}{1}.\frac{3}{u\sqrt[]{{u}^{2}-1}}.\frac{du}{3}](/latexrender/pictures/fce6437d1c4095b39b5eda37c3a9ccc7.png)
![\int_{}^{}\frac{1}{u\sqrt[]{{u}^{2}-1}}.du \int_{}^{}\frac{1}{u\sqrt[]{{u}^{2}-1}}.du](/latexrender/pictures/3e23f4a083f430fb38432bcca269ed0f.png)
- Paro nesta parte. Em suma, todos os itens do nº6 parecem dar neste mesmo problema. Eu não consigo tirar o
![u\sqrt[]{{u}^{2}-1} u\sqrt[]{{u}^{2}-1}](/latexrender/pictures/798b08b2792f6825aa0635f19f500ace.png)
do denominador e continuar.
Desde já grato pela atenção. Abraços.
Cordialmente, Matheus L. Oliveira.
-
Matheus Lacombe O
- Usuário Dedicado

-
- Mensagens: 36
- Registrado em: Sex Jun 03, 2011 22:37
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Eng. Mecânica
- Andamento: cursando
 por e8group » Dom Mar 03, 2013 16:02
por e8group » Dom Mar 03, 2013 16:02
Boa tarde ,parece ser mais prático o desenvolvimento da questão caso faça a substituição

;daí derivando ambos membros em relação x ,obtemos :
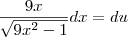
.
Deste modo fazendo as devidas substiuições ,temos
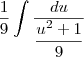
Consegue concluir ?
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Matheus Lacombe O » Dom Mar 03, 2013 17:19
por Matheus Lacombe O » Dom Mar 03, 2013 17:19
Sim, sim. O problema é que o exercício do Anton pede pro sujeito utilizar "u=3x". Dai da problema
-
Matheus Lacombe O
- Usuário Dedicado

-
- Mensagens: 36
- Registrado em: Sex Jun 03, 2011 22:37
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Eng. Mecânica
- Andamento: cursando
 por e8group » Dom Mar 03, 2013 18:15
por e8group » Dom Mar 03, 2013 18:15
Ok.,neste caso recomendo que faça

.Tente concluir .
OBS.: Veja que
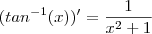
.
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Integral Indefinida] Método por Partes
por Matheus Lacombe O » Sex Mar 29, 2013 18:12
- 5 Respostas
- 2958 Exibições
- Última mensagem por young_jedi

Sáb Mar 30, 2013 21:33
Cálculo: Limites, Derivadas e Integrais
-
- Integral indefinida (por substituição)
por Anne2011 » Sex Set 16, 2011 21:00
- 5 Respostas
- 3327 Exibições
- Última mensagem por Anne2011

Sex Set 16, 2011 21:47
Cálculo: Limites, Derivadas e Integrais
-
- Integral indefinida (por substituição)
por Anne2011 » Sex Set 16, 2011 23:17
- 3 Respostas
- 2647 Exibições
- Última mensagem por MarceloFantini

Sáb Set 17, 2011 17:28
Cálculo: Limites, Derivadas e Integrais
-
- [INTEGRAL INDEFINIDA] Substituição
por fabriel » Qua Out 03, 2012 13:24
- 2 Respostas
- 2346 Exibições
- Última mensagem por fabriel

Qua Out 03, 2012 15:15
Cálculo: Limites, Derivadas e Integrais
-
- [INTEGRAL INDEFINIDA] Substituição
por fabriel » Seg Nov 26, 2012 00:03
- 4 Respostas
- 3247 Exibições
- Última mensagem por fabriel

Ter Nov 27, 2012 01:23
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\int_{}^{}\frac{1}{x\sqrt[]{9{x}^{2}-1}}dx \int_{}^{}\frac{1}{x\sqrt[]{9{x}^{2}-1}}dx](/latexrender/pictures/c1118fa067dab539f80f68636b31fa7f.png)
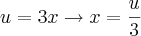


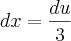
![\int_{}^{}\frac{1}{\frac{u\sqrt[]{{u}^{2}-1}}{3}}.\frac{du}{3} \int_{}^{}\frac{1}{\frac{u\sqrt[]{{u}^{2}-1}}{3}}.\frac{du}{3}](/latexrender/pictures/0dc0be322fd299ad9c298f433fc3dc80.png)
![\int_{}^{}\frac{1}{1}.\frac{3}{u\sqrt[]{{u}^{2}-1}}.\frac{du}{3} \int_{}^{}\frac{1}{1}.\frac{3}{u\sqrt[]{{u}^{2}-1}}.\frac{du}{3}](/latexrender/pictures/fce6437d1c4095b39b5eda37c3a9ccc7.png)
![\int_{}^{}\frac{1}{u\sqrt[]{{u}^{2}-1}}.du \int_{}^{}\frac{1}{u\sqrt[]{{u}^{2}-1}}.du](/latexrender/pictures/3e23f4a083f430fb38432bcca269ed0f.png)
![u\sqrt[]{{u}^{2}-1} u\sqrt[]{{u}^{2}-1}](/latexrender/pictures/798b08b2792f6825aa0635f19f500ace.png) do denominador e continuar.
do denominador e continuar.
![\int_{}^{}\frac{1}{x\sqrt[]{9{x}^{2}-1}}dx \int_{}^{}\frac{1}{x\sqrt[]{9{x}^{2}-1}}dx](/latexrender/pictures/c1118fa067dab539f80f68636b31fa7f.png)
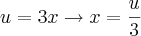


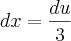
![\int_{}^{}\frac{1}{\frac{u\sqrt[]{{u}^{2}-1}}{3}}.\frac{du}{3} \int_{}^{}\frac{1}{\frac{u\sqrt[]{{u}^{2}-1}}{3}}.\frac{du}{3}](/latexrender/pictures/0dc0be322fd299ad9c298f433fc3dc80.png)
![\int_{}^{}\frac{1}{1}.\frac{3}{u\sqrt[]{{u}^{2}-1}}.\frac{du}{3} \int_{}^{}\frac{1}{1}.\frac{3}{u\sqrt[]{{u}^{2}-1}}.\frac{du}{3}](/latexrender/pictures/fce6437d1c4095b39b5eda37c3a9ccc7.png)
![\int_{}^{}\frac{1}{u\sqrt[]{{u}^{2}-1}}.du \int_{}^{}\frac{1}{u\sqrt[]{{u}^{2}-1}}.du](/latexrender/pictures/3e23f4a083f430fb38432bcca269ed0f.png)
![u\sqrt[]{{u}^{2}-1} u\sqrt[]{{u}^{2}-1}](/latexrender/pictures/798b08b2792f6825aa0635f19f500ace.png) do denominador e continuar.
do denominador e continuar.
 ;daí derivando ambos membros em relação x ,obtemos :
;daí derivando ambos membros em relação x ,obtemos : 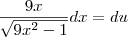 .
.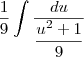


 .Tente concluir .
.Tente concluir . 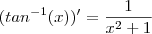 .
.


 substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.