![\int \frac{1}{\sqrt[3]{x} (\sqrt[3]{x} +1)}](/latexrender/pictures/5eb30feadef59a7cd6ab40743516fbfa.png "\int \frac{1}{\sqrt[3]{x} (\sqrt[3]{x} +1)}")
dxBom, meu professor nos explicou de um modo que eu teria que fazer o mmc com os denominadores da função , que neste caso seria 3 , logo x= z³
então
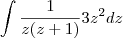
aí divido
3z² / z² + z = 3 , com um resto= -3z
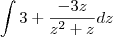
daí na segunda integral dessa última, faço por frações parciais , né?
o estranho é que se faço por frações parciais, fiz (A/z) + (B/z+1)
onde achei A= 1 e B=-1, mas a integral fica -3
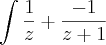
que resolvendo, resulta em -3 ln
![\left|\sqrt[3]{x} \right|](/latexrender/pictures/1f3eed8fe0e0843f72a00d0232af61fe.png "\left|\sqrt[3]{x} \right|")
+ c E 3ln![\left|\sqrt[3]{x} +1 \right|](/latexrender/pictures/67e4e83319498a5c142a733cc57cbe0b.png "\left|\sqrt[3]{x} +1 \right|")
+ c Só que somando com a integral do começo ( 3dz ) que me resultava em 3z+c = 3
![\sqrt[3]{x}](/latexrender/pictures/6833f4eaccfb60d5c13fdf6b6cc30aef.png "\sqrt[3]{x}")
+ c , o resultado final seria :
3
- 3 ln + 3ln + c Ou não??
o Resultado do meu professor e do wolfram foi: 3
+ 3ln + c
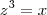obtemos :
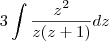que se resume em (após cancelarmos o fator 3 no numerador e denominador) 
. 
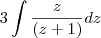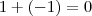no numerador .Segue que ,
que resulta 
. ![\int \frac{dx}{\sqrt[3]{x}(\sqrt[3]{x}+1)} = 3\sqrt[3]{x} - 3ln(\sqrt[3]{x} + 1) + c](/latexrender/pictures/fc5fa599e85d0a11ee0c6deac2411bff.png "\int \frac{dx}{\sqrt[3]{x}(\sqrt[3]{x}+1)} = 3\sqrt[3]{x} - 3ln(\sqrt[3]{x} + 1) + c")
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png "{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}")
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png "{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}")
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png "{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}")
da seguinte forma:
.
da seguinte forma:
.