 pelo método da substituição?
pelo método da substituição?

 pelo método da substituição?
pelo método da substituição?
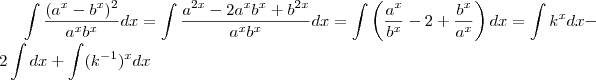

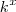 como
como 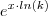 .(Assumindo que
.(Assumindo que  )
)
 ,(Para
,(Para 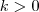 ),
),

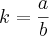


 do numerador da fração ?
do numerador da fração ?
 .
.  .
. (Verifique ! )
(Verifique ! )
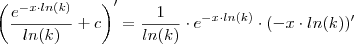
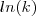 como sendo um constante e por isso não o derivou e também é por isso que
como sendo um constante e por isso não o derivou e também é por isso que 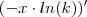 =
= 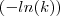 ?
? e substituindo o valor de
e substituindo o valor de  por
por  eu cheguei ao seguinte processo:
eu cheguei ao seguinte processo:
 antes da fração.
antes da fração.
 que está antes da fração?
que está antes da fração?
 é uma constante . Lembre-se
é uma constante . Lembre-se  e
e  são reais fixos(b
são reais fixos(b  ,que pela nossa hipótese
,que pela nossa hipótese 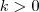 ) .
) . 

Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 7 visitantes
