Alguém pode mostrar uma forma prática para se afirmar se uma dada função é limitada ou não?
Por exemplo, a função
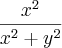 é limitada. Eu percebo isso intuitivamente. Mas gostaria de aprender uma forma de demonstrar formalmente.
é limitada. Eu percebo isso intuitivamente. Mas gostaria de aprender uma forma de demonstrar formalmente.Outro exemplo é a função
 . Esta não é limitada (vi em um livro). Porém nem intuitivamente consigo notar isso. Assim, gostaria de aprender uma técnica ou demonstração formal a fim de apontar se uma dada função é limitada ou não.
. Esta não é limitada (vi em um livro). Porém nem intuitivamente consigo notar isso. Assim, gostaria de aprender uma técnica ou demonstração formal a fim de apontar se uma dada função é limitada ou não.Desde já agradeço!


 definida por
definida por 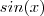 é limitada , pois
é limitada , pois 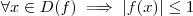 .Neste caso
.Neste caso ![Im(f) \in [-1
,1] \forall x \in \mathbb{R} Im(f) \in [-1
,1] \forall x \in \mathbb{R}](/latexrender/pictures/0e5691591058dca91edacd03190e1fa7.png) . Faça uma analogia com funções duas variáveis .
. Faça uma analogia com funções duas variáveis .  é uma função limitada .Primeiro note que ,
é uma função limitada .Primeiro note que ,  .Isto contradiz apenas quando
.Isto contradiz apenas quando 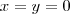 . Portanto se
. Portanto se  vamos ter
vamos ter 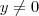 e vice-versa .
e vice-versa . 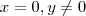 temos
temos  e para
e para 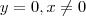 segue
segue 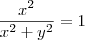 . Agora para
. Agora para  vamos ter que :
vamos ter que :  . Note que,
. Note que,  .Tome
.Tome  e
e 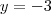 é fácil ver que
é fácil ver que 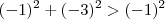 e assim sucessivamente .
e assim sucessivamente .  não podemos fazer a mesma afirmação .
não podemos fazer a mesma afirmação . 



 .
.
 :
: