a)
![\int_{0}^{1}\sqrt[]{1+x^2}dx\leq\int_{0}^{1}\sqrt[]{1+x}dx \int_{0}^{1}\sqrt[]{1+x^2}dx\leq\int_{0}^{1}\sqrt[]{1+x}dx](/latexrender/pictures/e608c0c3ad7f7260c185f5cf6c6306ea.png)
b)
![2\leq\int_{-1}^{1}\sqrt[]{1+x^2}dx\leq2\sqrt[]{2} 2\leq\int_{-1}^{1}\sqrt[]{1+x^2}dx\leq2\sqrt[]{2}](/latexrender/pictures/acc41d3f0160cee43792c05e2846cd21.png)
c)
![\frac{\sqrt[]{2}}{24}\Pi\leq\int_{\frac{\Pi}{6}}^{\frac{\Pi}{4}}cosxdx\leq\frac{\sqrt[]{3}}{24}\Pi \frac{\sqrt[]{2}}{24}\Pi\leq\int_{\frac{\Pi}{6}}^{\frac{\Pi}{4}}cosxdx\leq\frac{\sqrt[]{3}}{24}\Pi](/latexrender/pictures/776d6127ebea1b5e3533a9e57d30ed1b.png)
Não sei como resolver o exercicio

![\int_{0}^{1}\sqrt[]{1+x^2}dx\leq\int_{0}^{1}\sqrt[]{1+x}dx \int_{0}^{1}\sqrt[]{1+x^2}dx\leq\int_{0}^{1}\sqrt[]{1+x}dx](/latexrender/pictures/e608c0c3ad7f7260c185f5cf6c6306ea.png)
![2\leq\int_{-1}^{1}\sqrt[]{1+x^2}dx\leq2\sqrt[]{2} 2\leq\int_{-1}^{1}\sqrt[]{1+x^2}dx\leq2\sqrt[]{2}](/latexrender/pictures/acc41d3f0160cee43792c05e2846cd21.png)
![\frac{\sqrt[]{2}}{24}\Pi\leq\int_{\frac{\Pi}{6}}^{\frac{\Pi}{4}}cosxdx\leq\frac{\sqrt[]{3}}{24}\Pi \frac{\sqrt[]{2}}{24}\Pi\leq\int_{\frac{\Pi}{6}}^{\frac{\Pi}{4}}cosxdx\leq\frac{\sqrt[]{3}}{24}\Pi](/latexrender/pictures/776d6127ebea1b5e3533a9e57d30ed1b.png)

Claudin escreveu:Utilize as propriedades das integrais para verificar as desigualdades sem calcular as integrais
a)
b)
c)
Não sei como resolver o exercicio
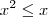

 e 1 + x serão números positivos. Podemos então aplicar a raiz quadrada em ambos os lados da inequação:
e 1 + x serão números positivos. Podemos então aplicar a raiz quadrada em ambos os lados da inequação: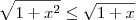

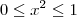

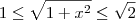
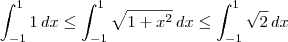
![\left[\frac{\pi}{6}, \frac{\pi}{4}\right] \left[\frac{\pi}{6}, \frac{\pi}{4}\right]](/latexrender/pictures/3cf28da642a88aaf74977af5b209c93a.png) , lembre-se que:
, lembre-se que: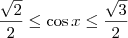

Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes


 , avisa que eu resolvo.
, avisa que eu resolvo.

