
Posso escreve-la assim, para decompor as frações:
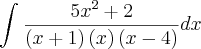
Então decompondo as frações, vamos ter o seguinte:

Isso vai nos levar ao seguinte:

Aí teremos o Sistema:

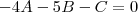

Logo:
 e
e 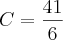
Teremos então:

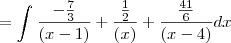
Calculando essa integral Vamos obter:
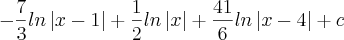
MAS AGORA EU POSSO SIMPLIFICAR ESSE RESULTADO?? SE SIM ENTÃO COMO QUE VAI FICAR??
(Um ótimo feriado a todos!!


