 por KleinIll » Qua Out 31, 2012 15:01
por KleinIll » Qua Out 31, 2012 15:01
![\lim_{x \rightarrow1} \left({x}^{3} - 1 \right)\left[ sen(\frac{1}{x - 1}) + cos(\frac{3}{x}) + 10 \right] \lim_{x \rightarrow1} \left({x}^{3} - 1 \right)\left[ sen(\frac{1}{x - 1}) + cos(\frac{3}{x}) + 10 \right]](/latexrender/pictures/0449cfe7dc25ebd58a0267e67f5fb21a.png)
Alguém pode explicar como resolver?
Reposta: 0
??? ?? ? ????, ? ? ??????.
-

KleinIll
- Usuário Dedicado

-
- Mensagens: 46
- Registrado em: Qua Out 31, 2012 14:17
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Engenharia Química
- Andamento: formado
 por young_jedi » Qua Out 31, 2012 20:33
por young_jedi » Qua Out 31, 2012 20:33
temos que para qualquer valor de x a expressção nos temos certeza que

esta entre -1 e 1 e
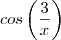
também ou seja:
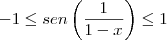
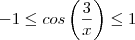
ou seja para quaquer valor de x maior que 1
![(x^3-1)(-1-1+10)<(x^3-1)\left[sen\left(\frac{1}{1-x}\right)+cos\left(\frac{3}{x}\right)+10\right] (x^3-1)(-1-1+10)<(x^3-1)\left[sen\left(\frac{1}{1-x}\right)+cos\left(\frac{3}{x}\right)+10\right]](/latexrender/pictures/3ccca9e15f643a1a27c6b4bd6e543073.png)
e
![(x^3-1)\left[sen\left(\frac{1}{1-x}\right)+cos\left(\frac{3}{x}\right\rihgt)+10\right]<(x^3-1)(1+1+10) (x^3-1)\left[sen\left(\frac{1}{1-x}\right)+cos\left(\frac{3}{x}\right\rihgt)+10\right]<(x^3-1)(1+1+10)](/latexrender/pictures/2972b20aca552558f59a759654ffac28.png)
ou seja
para valores de x>1 nos temos
![(x^3-1)8<(x^3-1)\left[sen\left(\frac{1}{1-x}\right)+cos\left(\frac{3}{x}\right\rihgt)+10\right]<(x^3-1)12 (x^3-1)8<(x^3-1)\left[sen\left(\frac{1}{1-x}\right)+cos\left(\frac{3}{x}\right\rihgt)+10\right]<(x^3-1)12](/latexrender/pictures/3018932e7c26731cb9579297db5b41c8.png)
mais nos temos que

e

então pelo teorema do confronto
![\lim_{x\rightarrow1_+}(x^3-1)\left[sen\left(\frac{1}{1-x}\right)+cos\left(\frac{3}{x}\right\rihgt)+10\right]=0 \lim_{x\rightarrow1_+}(x^3-1)\left[sen\left(\frac{1}{1-x}\right)+cos\left(\frac{3}{x}\right\rihgt)+10\right]=0](/latexrender/pictures/d9217826124b7fe33f78e944101c0b6e.png)
de forma semelhante nos temos que para x<1
![(x^3-1)(-1-1+10)>(x^3-1)\left[sen\left(\frac{1}{1-x}\right)+cos\left(\frac{3}{x}\right)+10\right] (x^3-1)(-1-1+10)>(x^3-1)\left[sen\left(\frac{1}{1-x}\right)+cos\left(\frac{3}{x}\right)+10\right]](/latexrender/pictures/32be94d1169153e340e7635301a96d72.png)
e
![(x^3-1)\left[sen\left(\frac{1}{1-x}\right)+cos\left(\frac{3}{x}\right\rihgt)+10\right]>(x^3-1)(1+1+10) (x^3-1)\left[sen\left(\frac{1}{1-x}\right)+cos\left(\frac{3}{x}\right\rihgt)+10\right]>(x^3-1)(1+1+10)](/latexrender/pictures/cf12410ce0a4b8d2aea3818037e0e03b.png)
ou seja
para valores de x<1 nos temos
![(x^3-1)8>(x^3-1)\left[sen\left(\frac{1}{1-x}\right)+cos\left(\frac{3}{x}\right\rihgt)+10\right]>(x^3-1)12 (x^3-1)8>(x^3-1)\left[sen\left(\frac{1}{1-x}\right)+cos\left(\frac{3}{x}\right\rihgt)+10\right]>(x^3-1)12](/latexrender/pictures/4738bfdafd367345f9ec1adc204a2b31.png)
mais nos temos que
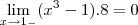
e

então pelo teorema do confronto
![\lim_{x\rightarrow1_-}(x^3-1)\left[sen\left(\frac{1}{1-x}\right)+cos\left(\frac{3}{x}\right\rihgt)+10\right]=0 \lim_{x\rightarrow1_-}(x^3-1)\left[sen\left(\frac{1}{1-x}\right)+cos\left(\frac{3}{x}\right\rihgt)+10\right]=0](/latexrender/pictures/d56a1197e9cfc76635d51b729ef79f67.png)
se os limites laterais existem e ambos são iguais a zero então o limite é igual a zero
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por e8group » Qua Out 31, 2012 20:34
por e8group » Qua Out 31, 2012 20:34
Desconsidere , já foi respondido .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Limite: Cosseno(x) e Seno(x) com X tendendo a infinito
por lucasguilherme2 » Qui Mai 24, 2012 11:49
- 3 Respostas
- 44433 Exibições
- Última mensagem por LuizAquino

Ter Mai 29, 2012 11:54
Cálculo: Limites, Derivadas e Integrais
-
- Seno e Cosseno de X??
por Leone de Paula » Ter Jul 13, 2010 00:28
- 1 Respostas
- 4656 Exibições
- Última mensagem por Tom

Ter Jul 13, 2010 00:43
Geometria Plana
-
- Lei do seno e cosseno
 por renataf » Sex Dez 03, 2010 11:06
por renataf » Sex Dez 03, 2010 11:06
- 7 Respostas
- 18807 Exibições
- Última mensagem por Lorettto

Sáb Dez 11, 2010 01:17
Trigonometria
-
- Seno e Cosseno
por karen » Qua Mai 16, 2012 22:20
- 1 Respostas
- 3708 Exibições
- Última mensagem por joaofonseca

Qui Mai 17, 2012 08:51
Trigonometria
-
- Seno e Cosseno
por Malorientado » Sáb Ago 18, 2012 17:55
- 1 Respostas
- 2766 Exibições
- Última mensagem por MarceloFantini

Sáb Ago 18, 2012 19:33
Trigonometria
Usuários navegando neste fórum: Nenhum usuário registrado e 11 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\lim_{x \rightarrow1} \left({x}^{3} - 1 \right)\left[ sen(\frac{1}{x - 1}) + cos(\frac{3}{x}) + 10 \right] \lim_{x \rightarrow1} \left({x}^{3} - 1 \right)\left[ sen(\frac{1}{x - 1}) + cos(\frac{3}{x}) + 10 \right]](/latexrender/pictures/0449cfe7dc25ebd58a0267e67f5fb21a.png)


 esta entre -1 e 1 e
esta entre -1 e 1 e 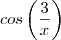 também ou seja:
também ou seja: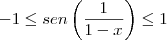
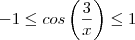
![(x^3-1)(-1-1+10)<(x^3-1)\left[sen\left(\frac{1}{1-x}\right)+cos\left(\frac{3}{x}\right)+10\right] (x^3-1)(-1-1+10)<(x^3-1)\left[sen\left(\frac{1}{1-x}\right)+cos\left(\frac{3}{x}\right)+10\right]](/latexrender/pictures/3ccca9e15f643a1a27c6b4bd6e543073.png)
![(x^3-1)\left[sen\left(\frac{1}{1-x}\right)+cos\left(\frac{3}{x}\right\rihgt)+10\right]<(x^3-1)(1+1+10) (x^3-1)\left[sen\left(\frac{1}{1-x}\right)+cos\left(\frac{3}{x}\right\rihgt)+10\right]<(x^3-1)(1+1+10)](/latexrender/pictures/2972b20aca552558f59a759654ffac28.png)
![(x^3-1)8<(x^3-1)\left[sen\left(\frac{1}{1-x}\right)+cos\left(\frac{3}{x}\right\rihgt)+10\right]<(x^3-1)12 (x^3-1)8<(x^3-1)\left[sen\left(\frac{1}{1-x}\right)+cos\left(\frac{3}{x}\right\rihgt)+10\right]<(x^3-1)12](/latexrender/pictures/3018932e7c26731cb9579297db5b41c8.png)


![\lim_{x\rightarrow1_+}(x^3-1)\left[sen\left(\frac{1}{1-x}\right)+cos\left(\frac{3}{x}\right\rihgt)+10\right]=0 \lim_{x\rightarrow1_+}(x^3-1)\left[sen\left(\frac{1}{1-x}\right)+cos\left(\frac{3}{x}\right\rihgt)+10\right]=0](/latexrender/pictures/d9217826124b7fe33f78e944101c0b6e.png)
![(x^3-1)(-1-1+10)>(x^3-1)\left[sen\left(\frac{1}{1-x}\right)+cos\left(\frac{3}{x}\right)+10\right] (x^3-1)(-1-1+10)>(x^3-1)\left[sen\left(\frac{1}{1-x}\right)+cos\left(\frac{3}{x}\right)+10\right]](/latexrender/pictures/32be94d1169153e340e7635301a96d72.png)
![(x^3-1)\left[sen\left(\frac{1}{1-x}\right)+cos\left(\frac{3}{x}\right\rihgt)+10\right]>(x^3-1)(1+1+10) (x^3-1)\left[sen\left(\frac{1}{1-x}\right)+cos\left(\frac{3}{x}\right\rihgt)+10\right]>(x^3-1)(1+1+10)](/latexrender/pictures/cf12410ce0a4b8d2aea3818037e0e03b.png)
![(x^3-1)8>(x^3-1)\left[sen\left(\frac{1}{1-x}\right)+cos\left(\frac{3}{x}\right\rihgt)+10\right]>(x^3-1)12 (x^3-1)8>(x^3-1)\left[sen\left(\frac{1}{1-x}\right)+cos\left(\frac{3}{x}\right\rihgt)+10\right]>(x^3-1)12](/latexrender/pictures/4738bfdafd367345f9ec1adc204a2b31.png)
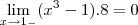

![\lim_{x\rightarrow1_-}(x^3-1)\left[sen\left(\frac{1}{1-x}\right)+cos\left(\frac{3}{x}\right\rihgt)+10\right]=0 \lim_{x\rightarrow1_-}(x^3-1)\left[sen\left(\frac{1}{1-x}\right)+cos\left(\frac{3}{x}\right\rihgt)+10\right]=0](/latexrender/pictures/d56a1197e9cfc76635d51b729ef79f67.png)



 .
.



