 por eli83 » Qua Out 31, 2012 10:50
por eli83 » Qua Out 31, 2012 10:50
Encontre a derivada da função dada, avaliando o valor aproximado de

para
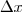
pequeno.
f(x) = x² + 3x +2
Bem, até encontrar a devirada tudo bem. Mas e avaliando o valor aproximado de

para
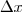
pequeno eu não entendi.
-
eli83
- Usuário Ativo

-
- Mensagens: 13
- Registrado em: Sáb Out 06, 2012 11:55
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática
- Andamento: formado
 por LuizAquino » Qui Nov 01, 2012 16:06
por LuizAquino » Qui Nov 01, 2012 16:06
eli83 escreveu:Encontre a derivada da função dada, avaliando o valor aproximado de

para
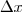
pequeno.
f(x) = x² + 3x +2
Bem, até encontrar a devirada tudo bem. Mas e avaliando o valor aproximado de

para
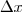
pequeno eu não entendi.
Suponha que

. Vamos considerar esse valor como sendo "pequeno" (o que é bem razoável).
Agora determine a expressão de
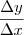
. Por exemplo, suponha que x variou de

até
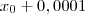
. Por definição, sabemos que

e
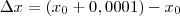
. Desse modo, você deve analisar a expressão:
![\dfrac{\Delta y}{\Delta x} = \dfrac{f(x_0+0,0001) - f(x_0)}{(x_0+0,0001) - x_0} = \dfrac{\left[\left(x_0+0,0001\right)^2 + 3\left(x_0+0,0001\right) + 2\right] - \left(x_0^2 + 3x_0 + 2\right)}{0,0001} \dfrac{\Delta y}{\Delta x} = \dfrac{f(x_0+0,0001) - f(x_0)}{(x_0+0,0001) - x_0} = \dfrac{\left[\left(x_0+0,0001\right)^2 + 3\left(x_0+0,0001\right) + 2\right] - \left(x_0^2 + 3x_0 + 2\right)}{0,0001}](/latexrender/pictures/40d32fe740a676dbcaaccd1696944a51.png)
Agora tente continuar a partir daí.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Aplicações de Derivada [Teorema do valor médio]
por xanda2012 » Sáb Jun 16, 2012 16:22
- 2 Respostas
- 2266 Exibições
- Última mensagem por xanda2012

Sáb Jun 16, 2012 17:43
Cálculo: Limites, Derivadas e Integrais
-
- [Valor de Mercadoria] A partir do valor total de venda
por Gerson Belini » Qua Out 02, 2013 02:17
- 0 Respostas
- 3906 Exibições
- Última mensagem por Gerson Belini

Qua Out 02, 2013 02:17
Matemática Financeira
-
- [Calcule o valor de Seno de 18º] Expressar o valor numérico
por VictorFPS » Sáb Fev 14, 2015 20:01
- 1 Respostas
- 3869 Exibições
- Última mensagem por adauto martins

Qui Fev 19, 2015 15:41
Trigonometria
-
- valor bruto a partir do valor liquido
por juan cunha » Ter Mai 03, 2016 10:29
- 3 Respostas
- 17804 Exibições
- Última mensagem por nakagumahissao

Sáb Mai 07, 2016 22:51
Matemática Financeira
-
- Valor de i que maximiza o valor do lucro
por filipeferminiano » Qui Jun 23, 2011 14:41
- 3 Respostas
- 4593 Exibições
- Última mensagem por LuizAquino

Sáb Ago 27, 2011 22:45
Cálculo
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 para
para 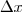 pequeno.
pequeno. para
para 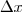 pequeno eu não entendi.
pequeno eu não entendi.
 para
para 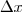 pequeno.
pequeno. para
para 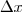 pequeno eu não entendi.
pequeno eu não entendi.
para
pequeno.
para
pequeno eu não entendi.
 . Vamos considerar esse valor como sendo "pequeno" (o que é bem razoável).
. Vamos considerar esse valor como sendo "pequeno" (o que é bem razoável).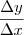 . Por exemplo, suponha que x variou de
. Por exemplo, suponha que x variou de  até
até 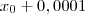 . Por definição, sabemos que
. Por definição, sabemos que  e
e 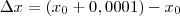 . Desse modo, você deve analisar a expressão:
. Desse modo, você deve analisar a expressão:![\dfrac{\Delta y}{\Delta x} = \dfrac{f(x_0+0,0001) - f(x_0)}{(x_0+0,0001) - x_0} = \dfrac{\left[\left(x_0+0,0001\right)^2 + 3\left(x_0+0,0001\right) + 2\right] - \left(x_0^2 + 3x_0 + 2\right)}{0,0001} \dfrac{\Delta y}{\Delta x} = \dfrac{f(x_0+0,0001) - f(x_0)}{(x_0+0,0001) - x_0} = \dfrac{\left[\left(x_0+0,0001\right)^2 + 3\left(x_0+0,0001\right) + 2\right] - \left(x_0^2 + 3x_0 + 2\right)}{0,0001}](/latexrender/pictures/40d32fe740a676dbcaaccd1696944a51.png)



 substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.