 por staltux » Seg Out 25, 2010 14:54
por staltux » Seg Out 25, 2010 14:54
bom pessoal, meu problema nem é tanto quanto ao criterio da razão propriamente dito, e sim com a matematica basica envolvida no meio...empaquei logo no começo, vou mostrar aqui as unicas coisas que consegui fazer...
O exercicio pede para dizer se converge(L<1) ou diverge(L>1).

entãm tentei deixar como pede a formula:
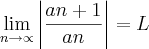
ficando:

entam fiz dividendo X inverso do divisor:
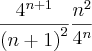
e é ai que o bixo pego pro meu lado, as unicas informações que sei é que

o que não me ajudou em nada, eu até pensei em fazer a parter de produtos notaveis do primeiro grupo, mas só piorou.
fica aqui onde chegeui com produtos notaveis:
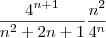
eu fiz besteira pro meio do caminho ou não? se não, como continuo,pois se aplicar o limite agora não vai funcionar.
-
staltux
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Seg Out 25, 2010 14:11
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciência da Computação
- Andamento: cursando
 por andrefahl » Sex Out 29, 2010 12:59
por andrefahl » Sex Out 29, 2010 12:59
Cara, eu acho que vc chegou bem perto
repare só:
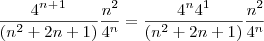
Agira o

cancela com o

ficando o seguinte
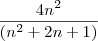
para calcular o limite divide tudo pela maior potencia

agora eh só calcular o limite que resulta em 4 =)
dai o limite é maior que 1
-
andrefahl
- Usuário Dedicado

-
- Mensagens: 36
- Registrado em: Qui Out 28, 2010 18:05
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Física - UNICAMP
- Andamento: cursando
 por staltux » Sex Out 29, 2010 13:23
por staltux » Sex Out 29, 2010 13:23
muito obrigado!
é por isso que o meu professor vive falando que agente não erra analise matematica, agente erra 7ª serie

eu simplesmente ignorei o fato de que se podia cortar os
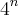
.
Burro burro burro, da 0 pra ele

-
staltux
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Seg Out 25, 2010 14:11
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciência da Computação
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Calculo 3: Critério da raiz
por Shuhey » Ter Abr 28, 2009 16:21
- 4 Respostas
- 4217 Exibições
- Última mensagem por Shuhey

Qua Abr 29, 2009 23:12
Cálculo: Limites, Derivadas e Integrais
-
- P.A de razão sendo outra P.A, ajuda
por MariMari » Qui Set 30, 2010 18:55
- 2 Respostas
- 2328 Exibições
- Última mensagem por MariMari

Sex Out 01, 2010 15:40
Progressões
-
- Ajuda juros simples
por crismara » Seg Dez 06, 2010 11:38
- 0 Respostas
- 1300 Exibições
- Última mensagem por crismara

Seg Dez 06, 2010 11:38
Matemática Financeira
-
- ajuda juros simples
por karlinhaa » Seg Dez 06, 2010 15:48
- 2 Respostas
- 1721 Exibições
- Última mensagem por karlinhaa

Ter Dez 07, 2010 10:34
Matemática Financeira
-
- [Juros Simples] Ajuda, por favor!
por Ronaldobb » Qui Fev 07, 2013 11:28
- 4 Respostas
- 4778 Exibições
- Última mensagem por DanielFerreira

Dom Fev 10, 2013 21:11
Matemática Financeira
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.

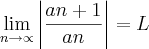

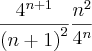

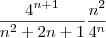


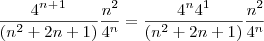
 cancela com o
cancela com o 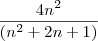


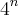 .
.