O exercicio pede para dizer se converge(L<1) ou diverge(L>1).

entãm tentei deixar como pede a formula:
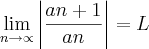
ficando:

entam fiz dividendo X inverso do divisor:
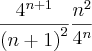
e é ai que o bixo pego pro meu lado, as unicas informações que sei é que

o que não me ajudou em nada, eu até pensei em fazer a parter de produtos notaveis do primeiro grupo, mas só piorou.
fica aqui onde chegeui com produtos notaveis:
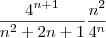
eu fiz besteira pro meio do caminho ou não? se não, como continuo,pois se aplicar o limite agora não vai funcionar.


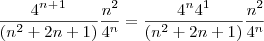
 cancela com o
cancela com o 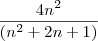


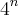 .
.