por Bruhh » Sáb Ago 07, 2010 14:49
por Bruhh » Sáb Ago 07, 2010 14:49
Olá

Então, eu estava resolvendo uma lista de exercícios mas alguns deles eu não consigo chegar ao resultado correto de jeito nenhum!
Fiz e refiz diversas vezes, mas não sei o que estou fazendo errado.
Segue abaixo uma integral das quais eu não consigo resolver:
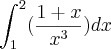
=
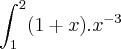
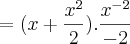

![=[(2+\frac{{2}^{2}}{2}).(-\frac{1}{2}).\frac{1}{{2}^{2}}] =[(2+\frac{{2}^{2}}{2}).(-\frac{1}{2}).\frac{1}{{2}^{2}}]](/latexrender/pictures/d7e4e9bf778bd9ab9d5d2b53a8905995.png)
-
![[(1+\frac{{1}^{2}}{2}).(-\frac{1}{2}).\frac{1}{{1}^{2}}] [(1+\frac{{1}^{2}}{2}).(-\frac{1}{2}).\frac{1}{{1}^{2}}]](/latexrender/pictures/2f77b52e1389184653d0d037283a85f6.png)
![=[4.(-\frac{1}{2}).\frac{1}{4}] =[4.(-\frac{1}{2}).\frac{1}{4}]](/latexrender/pictures/6db4cd4cda9f224ffe0f1bfec3e40583.png)
-
![[\frac{3}{2}.(-\frac{1}{2}).1] [\frac{3}{2}.(-\frac{1}{2}).1]](/latexrender/pictures/2c16bcf87063708446fd91d66ff3943f.png)
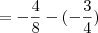
=

-O resultado deve ser

-------------------------------------------------------------



----------------------------------------------------------------------------------------
Se alguém puder me ajudar eu agradeço muito.
Obrigada
Bom final de semana a todos!!
-
Bruhh
- Usuário Dedicado

-
- Mensagens: 47
- Registrado em: Seg Mar 01, 2010 14:30
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Bacharelado em Eng. Química
- Andamento: cursando
 por Molina » Sáb Ago 07, 2010 16:38
por Molina » Sáb Ago 07, 2010 16:38
Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por Bruhh » Sáb Ago 07, 2010 20:07
por Bruhh » Sáb Ago 07, 2010 20:07
Ah você não deve ter endentido minha resolução simplesmente porque eu fiz uma "coisa de outro mundo", haha

Mas já entendi o que eu estou fazendo de errado.
Eu estava resolvendo a integral antes de multiplicar o
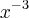
por

. Aí a resolução fica completamente errada.
Muito Obrigada

-
Bruhh
- Usuário Dedicado

-
- Mensagens: 47
- Registrado em: Seg Mar 01, 2010 14:30
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Bacharelado em Eng. Química
- Andamento: cursando
 por Molina » Dom Ago 08, 2010 15:04
por Molina » Dom Ago 08, 2010 15:04
Bruhh escreveu:Ah você não deve ter endentido minha resolução simplesmente porque eu fiz uma "coisa de outro mundo", haha

Mas já entendi o que eu estou fazendo de errado.
Eu estava resolvendo a integral antes de multiplicar o
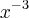
por

. Aí a resolução fica completamente errada.
Muito Obrigada

Ok, Bruhh.
Só lembre-se que a integral da multiplicação
não é a multiplicação das integrais. Ou seja:
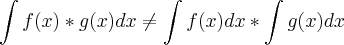
Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [integrais] Calculando áreas - Integrais
 por Faby » Seg Set 19, 2011 10:55
por Faby » Seg Set 19, 2011 10:55
- 11 Respostas
- 8811 Exibições
- Última mensagem por LuizAquino

Qua Set 21, 2011 18:03
Cálculo: Limites, Derivadas e Integrais
-
- Integrais
por pseytow » Qui Nov 27, 2008 21:54
- 1 Respostas
- 2805 Exibições
- Última mensagem por Adriano Tavares

Qui Mar 10, 2011 01:52
Cálculo: Limites, Derivadas e Integrais
-
- Integrais
por panneitz » Dom Jun 07, 2009 19:55
- 1 Respostas
- 2437 Exibições
- Última mensagem por Marcampucio

Dom Jun 07, 2009 20:31
Cálculo: Limites, Derivadas e Integrais
-
- Integrais
por leha » Ter Nov 10, 2009 16:08
- 2 Respostas
- 2520 Exibições
- Última mensagem por leha

Sex Nov 13, 2009 08:56
Cálculo: Limites, Derivadas e Integrais
-
- Integrais em IR3
por Saruman » Sáb Mai 22, 2010 10:27
- 1 Respostas
- 2133 Exibições
- Última mensagem por luispereira

Ter Dez 28, 2010 01:45
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 9 visitantes
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.

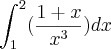 =
= 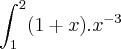
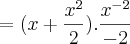

![=[(2+\frac{{2}^{2}}{2}).(-\frac{1}{2}).\frac{1}{{2}^{2}}] =[(2+\frac{{2}^{2}}{2}).(-\frac{1}{2}).\frac{1}{{2}^{2}}]](/latexrender/pictures/d7e4e9bf778bd9ab9d5d2b53a8905995.png) -
-![[(1+\frac{{1}^{2}}{2}).(-\frac{1}{2}).\frac{1}{{1}^{2}}] [(1+\frac{{1}^{2}}{2}).(-\frac{1}{2}).\frac{1}{{1}^{2}}]](/latexrender/pictures/2f77b52e1389184653d0d037283a85f6.png)
![=[4.(-\frac{1}{2}).\frac{1}{4}] =[4.(-\frac{1}{2}).\frac{1}{4}]](/latexrender/pictures/6db4cd4cda9f224ffe0f1bfec3e40583.png) -
-![[\frac{3}{2}.(-\frac{1}{2}).1] [\frac{3}{2}.(-\frac{1}{2}).1]](/latexrender/pictures/2c16bcf87063708446fd91d66ff3943f.png)
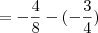




 ----------------------------------------------------------------------------------------
----------------------------------------------------------------------------------------




![=\left[-\frac{x^{-2}}{2}-x^{-1} \right]^2_1= =\left[-\frac{x^{-2}}{2}-x^{-1} \right]^2_1=](/latexrender/pictures/ae88387cf4b8c20746397c9a4fad6955.png)
![=\left[-\frac{1}{2x^2}-\frac{1}{x} \right]^2_1= =\left[-\frac{1}{2x^2}-\frac{1}{x} \right]^2_1=](/latexrender/pictures/724d113ae9bb4dbeb4af711e95e4e131.png)
![=\left[-\frac{1}{8}-\frac{1}{2} \right]-\left[-\frac{1}{2}-1 \right]= =\left[-\frac{1}{8}-\frac{1}{2} \right]-\left[-\frac{1}{2}-1 \right]=](/latexrender/pictures/dfad720850cbfd3ff79eeb5f69a34f00.png)
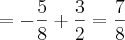

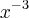 por
por  . Aí a resolução fica completamente errada.
. Aí a resolução fica completamente errada.