CARAMBA EU TENHO QUE ENTREGAR UMAS QUESTÕES SEGUNDA FEIRA E EU NÃO CONSEQUI FAZER ALGUMAS ..E OUTRAS EU ATÉ QUE CONSEGUI.
ME AJUDEM A FAZER O QUE FALTA E VEJAM SE AS QUE EU FIZ ESTÃO OK.
1ª EQUAÇÃO DA TANGENETE ?
>>Y= TG({-X}^{2}+1), X=1
>>Y=COS(frac{X}{2}) , X = 1
ESSA EU REPONDI ASSIM:

2ª UM CARTAZ DEVE CONTER 50CM² DE MATERIA IMPRESSSA COM DUAS MARGENS DE 4 CM CADA, NA PARTE SUPERIOR E NA PARTE INFERIOR E DUAS MARGENS LATERAISDE 2 CM CADA. DETERMINE AS DIMENSOÊS?
3ª DETERMINE O MAIOR COMPRIMENTO QUE DEVE TER UMA ESCADA PARA PASSAR DE UM CORREDOR DE 5 METROS DE LARGURA A OUTRO, PERPENDICULAR, DE 8 METROS DE LARGURA?
4CALCULE Y'
![Y=\sqrt[2]{2-{COS}^{2}(X)}
Y=\sqrt[2]{1-{TG}^{2}(X)}
Y={LOG}_{A}(IN(X))
Y=COT(SEC({X}^{2})
Y=\frac{SEN(2X)}{1+COS2X} Y=\sqrt[2]{2-{COS}^{2}(X)}
Y=\sqrt[2]{1-{TG}^{2}(X)}
Y={LOG}_{A}(IN(X))
Y=COT(SEC({X}^{2})
Y=\frac{SEN(2X)}{1+COS2X}](/latexrender/pictures/864d4a91a6f6c34d4b632aaf9b1c3194.png)
NÃO PRESCISA RESPONDER TODAS UMA OU DUAS OU ATE MESMO TODAS(É O QUE EU QUERO) JAH IA ME AJUDAR A NÃO REPETI A CADEIRA DE CALCULO INTEGRAL E DIFERNCIAL
ME AJUDEM PELO AMOR DE DEUS
E CASO DE VIDA OU REPEDIR O PERIODO




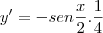
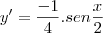







 e
e 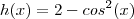 , então
, então  e usando a Regra da Cadeia:
e usando a Regra da Cadeia: 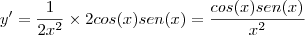
 é totalmente análogo ao item
é totalmente análogo ao item  , basta modificar durante a derivação da função interna.
, basta modificar durante a derivação da função interna. não dá pra entender o que você digiou, infelizmente.
não dá pra entender o que você digiou, infelizmente.
 e
e 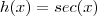 e
e 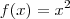 , então
, então 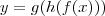 e usando a Regra da Cadeia:
e usando a Regra da Cadeia:![y'=g'(h(f(x))).[h(f(x))]'=g'(h(f(x))).h'(f(x)).f'(x) y'=g'(h(f(x))).[h(f(x))]'=g'(h(f(x))).h'(f(x)).f'(x)](/latexrender/pictures/a02deca9b5a12083f1113ac6e0d95a61.png)
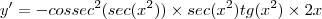

 . O "raio de sol" que os ilumina feixa dois triângulos retângulos semelhantes, pois contêm ângulos iguais, de catetos:
. O "raio de sol" que os ilumina feixa dois triângulos retângulos semelhantes, pois contêm ângulos iguais, de catetos: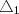 : Altura do homem , sombra do homem.
: Altura do homem , sombra do homem.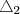 : Altura do poste, (sombra do homem+distância entre o homem e o poste).
: Altura do poste, (sombra do homem+distância entre o homem e o poste). o comprimento da sombra, da semelhança dos triângulos, temos:
o comprimento da sombra, da semelhança dos triângulos, temos: e decorre em
e decorre em  , isto é,
, isto é, 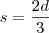
 , então vou resolver com essa consideração.
, então vou resolver com essa consideração. , concluímos que o gráfico é uma parábola.
, concluímos que o gráfico é uma parábola. , concluímos que é uma parábola com concavidade voltada para baixo.
, concluímos que é uma parábola com concavidade voltada para baixo. , concluímos que a curva não intercepta o eixo
, concluímos que a curva não intercepta o eixo 
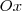
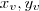 ) para saber as coordenadas do ponto onde o objeto atinge a altura máxima.
) para saber as coordenadas do ponto onde o objeto atinge a altura máxima.
 e o instante em que ela é atingida é o
e o instante em que ela é atingida é o 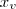 .
.

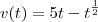
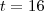 significa obter a derivada da função no ponto
significa obter a derivada da função no ponto 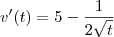 , entao
, entao 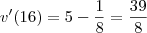
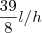


![A) y = {x}^{8} + {(2x + 4)}^{3} +\sqrt[]{x}
C) y = 3x(8x{}^{3} -2)
D) y = \sqrt[3]{6x{}^{2} + 7x + 2}
E) f(x) = 10(3x{}^{2} + 7x -3){}^{10}
F) f(x)= (x{}^{5} - 4x{}^{3} - 7){}^{8} A) y = {x}^{8} + {(2x + 4)}^{3} +\sqrt[]{x}
C) y = 3x(8x{}^{3} -2)
D) y = \sqrt[3]{6x{}^{2} + 7x + 2}
E) f(x) = 10(3x{}^{2} + 7x -3){}^{10}
F) f(x)= (x{}^{5} - 4x{}^{3} - 7){}^{8}](/latexrender/pictures/1c35090de08712f5410d87d584f303ab.png)
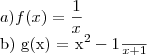
 , foi usada a Regra da Cadeia e a Regra de derivação de funções polinomiais.
, foi usada a Regra da Cadeia e a Regra de derivação de funções polinomiais.
 , foi usada a Regra do Produto e a Regra da função polinomial.
, foi usada a Regra do Produto e a Regra da função polinomial. , foi usada a Regra da Cadeia e a Regra de derivação de funções polinomiais.
, foi usada a Regra da Cadeia e a Regra de derivação de funções polinomiais.![E)(10)'[(3x^2+7x-3)^{10}]+10[(3x^2+7x-3)^{10}]'=10.10(3x^2+7x-3)^9(6x+7) E)(10)'[(3x^2+7x-3)^{10}]+10[(3x^2+7x-3)^{10}]'=10.10(3x^2+7x-3)^9(6x+7)](/latexrender/pictures/9813c6939a2195aaf841762513220827.png) , foram usadas as regras : Do Produto, Da Cadeia, Das funções polinomiais.
, foram usadas as regras : Do Produto, Da Cadeia, Das funções polinomiais.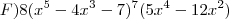 , foi usada a Regra da Cadeia e a Regra de derivação de funções polinomiais.
, foi usada a Regra da Cadeia e a Regra de derivação de funções polinomiais.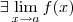 e
e 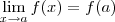
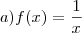 , percebemos que
, percebemos que 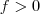 se
se  e
e 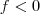 se
se 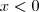 , no entanto,
, no entanto,  . Observa-se que os limites laterais de
. Observa-se que os limites laterais de  para
para 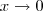 são distintos, portanto não existe limite para
são distintos, portanto não existe limite para  é abicissa do ponto de descontinuidade e a função é, notavelmente, descontínua.
é abicissa do ponto de descontinuidade e a função é, notavelmente, descontínua. e como não estamos interessados em tornar
e como não estamos interessados em tornar 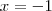 mas se em verificar o limite quando tendemos
mas se em verificar o limite quando tendemos  ao valor supracitado, temos que:
ao valor supracitado, temos que:  e há, notavelmente o limite para
e há, notavelmente o limite para  .
. é contínua.
é contínua.

 , avisa que eu resolvo.
, avisa que eu resolvo.

