 por CloudP4 » Seg Jun 28, 2010 22:08
por CloudP4 » Seg Jun 28, 2010 22:08
Tentei mas não conseguir fazer os seguintes limites:
![\lim_{x \rightarrow 1} \frac{\sqrt[]{x} - 1}{\sqrt[]{2x+3} - \sqrt[]{5}} \lim_{x \rightarrow 1} \frac{\sqrt[]{x} - 1}{\sqrt[]{2x+3} - \sqrt[]{5}}](/latexrender/pictures/e05a915229d57e3b888e016056a6d24c.png)
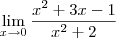
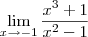
![\lim_{x \rightarrow 7} \frac{\sqrt[]{x} - \sqrt[]{7}}{\sqrt[]{x + 7} - \sqrt[]{14}} \lim_{x \rightarrow 7} \frac{\sqrt[]{x} - \sqrt[]{7}}{\sqrt[]{x + 7} - \sqrt[]{14}}](/latexrender/pictures/cca90b1c02de48af919ea504cc0bb43e.png)
E quem puder me explicar, como identifico o limite pelo método intuitivo, conforme mostra a img abaixo:

Desculpe um pouco o excesso, mas essas são mihas dúvidas no momento.
Obs: Ainda não cheguei a ver derivada.
-
CloudP4
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Seg Jun 07, 2010 23:45
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Eng. Civil
- Andamento: cursando
 por Neperiano » Seg Jun 28, 2010 22:48
por Neperiano » Seg Jun 28, 2010 22:48
Oi
Quanto aos primeiros limites, primeiro substitua o valor de x embaixo do lim, nas equações e va resolvendo, caso voce encontre o dividido por 0, isso é indice de indeterminação, por isso voce deve dar um jeito de cortar, fatorar a equação, não vou entrar nisso agora, deixe voce pensar um pouco.
Quanto ao gráfico voce deve analisar para onde a curva esta indo, por exemplo no ponto 3- o valor de y é 7 pois a curva pela esquerda vem dali, e quando em um ponto há dois limites e não é dado o lado a olhar a resposta é que esta indeterminado o limite naquele ponto, representada pela letra e virada com um tração emcima
Qualquer duvida
Espero ter ajudado
Sómente os mortos conhecem o fim da guerra
"Platão"
-

Neperiano
- Colaborador Voluntário

-
- Mensagens: 960
- Registrado em: Seg Jun 16, 2008 17:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
 por MarceloFantini » Seg Jun 28, 2010 23:28
por MarceloFantini » Seg Jun 28, 2010 23:28
O primeiro e o quarto são chatos. Vou apenas dizer como fazer e você faça as contas (já fiz e deu certo, estou com preguiça de escrever com Latex).
No primeiro, multiplique em cima pelo "conjugado" (
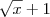
), e depois embaixo pelo conjugado também. Verá que o (x-1) pode ser cancelado, e aí o limite não é mais indeterminado. O quarto é feito de maneira análoga.
O segundo é fácil, basta jogar 0 no limite.
No terceiro, fatore as expressões do numerador e do denominador, alguma coisa cancelará.
Com relação ao gráfico, apenas veja intuitivamente para qual valor a função se aproxima. Se dos dois lados se aproximar do mesmo valor, o limite existe. Caso contrário, não.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por PeIdInHu » Qua Jul 07, 2010 22:33
por PeIdInHu » Qua Jul 07, 2010 22:33
.
-
PeIdInHu
- Usuário Ativo

-
- Mensagens: 16
- Registrado em: Sáb Mai 22, 2010 14:47
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Imformatica Biomedica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Limite] Gráfico e limite para função maior inteiro
 por Raphaela_sf » Qui Abr 05, 2012 19:26
por Raphaela_sf » Qui Abr 05, 2012 19:26
- 1 Respostas
- 6642 Exibições
- Última mensagem por LuizAquino

Qui Abr 05, 2012 20:53
Cálculo: Limites, Derivadas e Integrais
-
- [Limite] Limite de funções reais de várias variáveis
por Bianca_R » Dom Nov 04, 2012 17:17
- 1 Respostas
- 4786 Exibições
- Última mensagem por MarceloFantini

Dom Nov 04, 2012 19:37
Cálculo: Limites, Derivadas e Integrais
-
- [Limite trigonométrico] Como calculo este limite?
por Ronaldobb » Qua Nov 07, 2012 23:14
- 3 Respostas
- 5117 Exibições
- Última mensagem por Ronaldobb

Qui Nov 08, 2012 07:37
Cálculo: Limites, Derivadas e Integrais
-
- [Limite] limite trigonométrico quando x tende ao infinito
por Ge_dutra » Seg Jan 28, 2013 10:13
- 2 Respostas
- 7257 Exibições
- Última mensagem por Ge_dutra

Ter Jan 29, 2013 14:20
Cálculo: Limites, Derivadas e Integrais
-
- [Limite] Limite de funções piso (maior inteiro)
por ViniciusAlmeida » Sáb Fev 14, 2015 10:09
- 2 Respostas
- 4434 Exibições
- Última mensagem por adauto martins

Qui Fev 19, 2015 15:01
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\lim_{x \rightarrow 1} \frac{\sqrt[]{x} - 1}{\sqrt[]{2x+3} - \sqrt[]{5}} \lim_{x \rightarrow 1} \frac{\sqrt[]{x} - 1}{\sqrt[]{2x+3} - \sqrt[]{5}}](/latexrender/pictures/e05a915229d57e3b888e016056a6d24c.png)
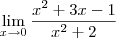
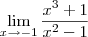
![\lim_{x \rightarrow 7} \frac{\sqrt[]{x} - \sqrt[]{7}}{\sqrt[]{x + 7} - \sqrt[]{14}} \lim_{x \rightarrow 7} \frac{\sqrt[]{x} - \sqrt[]{7}}{\sqrt[]{x + 7} - \sqrt[]{14}}](/latexrender/pictures/cca90b1c02de48af919ea504cc0bb43e.png)


![\lim_{x \rightarrow 1} \frac{\sqrt[]{x} - 1}{\sqrt[]{2x+3} - \sqrt[]{5}} \lim_{x \rightarrow 1} \frac{\sqrt[]{x} - 1}{\sqrt[]{2x+3} - \sqrt[]{5}}](/latexrender/pictures/e05a915229d57e3b888e016056a6d24c.png)
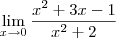
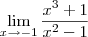
![\lim_{x \rightarrow 7} \frac{\sqrt[]{x} - \sqrt[]{7}}{\sqrt[]{x + 7} - \sqrt[]{14}} \lim_{x \rightarrow 7} \frac{\sqrt[]{x} - \sqrt[]{7}}{\sqrt[]{x + 7} - \sqrt[]{14}}](/latexrender/pictures/cca90b1c02de48af919ea504cc0bb43e.png)



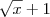 ), e depois embaixo pelo conjugado também. Verá que o (x-1) pode ser cancelado, e aí o limite não é mais indeterminado. O quarto é feito de maneira análoga.
), e depois embaixo pelo conjugado também. Verá que o (x-1) pode ser cancelado, e aí o limite não é mais indeterminado. O quarto é feito de maneira análoga.

