 por ezidia51 » Dom Set 29, 2019 19:53
por ezidia51 » Dom Set 29, 2019 19:53
tentei resolver estas duas questões de cálculo mas fiquei perdida.Quem puder ajudar ficarei muito agradecida
1)A área da região do plano do gráfico da função f(x)=cos(2x),acima do eixo ox para x
![x\in\left[0,\frac{\pi}{4} \right] x\in\left[0,\frac{\pi}{4} \right]](/latexrender/pictures/9777991a6d6332f17d8be9643bf9211d.png)
é?Como posso calcular esta área????
2)Uma particula se desloca sobre o eixo ox com velocidade em função do tempo,dada por v(t)=
![\sqrt[]{t}+3,t\geq 0. \sqrt[]{t}+3,t\geq 0.](/latexrender/pictures/f96e0a66b59ce9763b9709d3d7e92748.png)
.O deslocamento dessa particula entre os instantes t -1 t -4 ??? Substitui na xpressão e depois subtrai tudo?Fiquei perdida nos cálculos
-
ezidia51
- Colaborador Voluntário

-
- Mensagens: 104
- Registrado em: Seg Mar 12, 2018 20:57
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: tecnico em enfermagem
- Andamento: formado
 por adauto martins » Seg Set 30, 2019 14:36
por adauto martins » Seg Set 30, 2019 14:36
1)
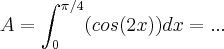
faz-se u=2x e...
2)
![v(x)=(dx/dt)=\sqrt[]{t}+3\Rightarrow dx=\sqrt[]{t}dt+3dt
x=\int_{t-1}^{t-4}(\sqrt[]{t}dt+3dt)=... v(x)=(dx/dt)=\sqrt[]{t}+3\Rightarrow dx=\sqrt[]{t}dt+3dt
x=\int_{t-1}^{t-4}(\sqrt[]{t}dt+3dt)=...](/latexrender/pictures/ad342cd95df77b7e4519b80b755019e6.png)
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
 por ezidia51 » Seg Set 30, 2019 17:28
por ezidia51 » Seg Set 30, 2019 17:28
-
ezidia51
- Colaborador Voluntário

-
- Mensagens: 104
- Registrado em: Seg Mar 12, 2018 20:57
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: tecnico em enfermagem
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Calculo] Lei da função a partir do grafico
 por deosdete » Dom Jun 10, 2012 16:29
por deosdete » Dom Jun 10, 2012 16:29
- 4 Respostas
- 3304 Exibições
- Última mensagem por LuizAquino

Ter Jun 12, 2012 12:37
Cálculo: Limites, Derivadas e Integrais
-
- Cálculo I - Gráfico
por Hel » Sáb Jan 09, 2010 15:52
- 0 Respostas
- 1926 Exibições
- Última mensagem por Hel

Sáb Jan 09, 2010 15:52
Cálculo: Limites, Derivadas e Integrais
-
- Calculo 1: Grafico
por Piva » Qua Jun 29, 2011 19:13
- 0 Respostas
- 1410 Exibições
- Última mensagem por Piva

Qua Jun 29, 2011 19:13
Cálculo: Limites, Derivadas e Integrais
-
- [calculo] esboço de gráfico
por beel » Ter Nov 01, 2011 16:16
- 1 Respostas
- 2166 Exibições
- Última mensagem por LuizAquino

Ter Nov 01, 2011 16:29
Cálculo: Limites, Derivadas e Integrais
-
- [Diferenciabilidade] Calculo e Gráfico
por urso » Ter Abr 22, 2014 11:08
- 3 Respostas
- 2653 Exibições
- Última mensagem por urso

Qua Abr 23, 2014 12:24
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 6 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![x\in\left[0,\frac{\pi}{4} \right] x\in\left[0,\frac{\pi}{4} \right]](/latexrender/pictures/9777991a6d6332f17d8be9643bf9211d.png) é?Como posso calcular esta área????
é?Como posso calcular esta área????![\sqrt[]{t}+3,t\geq 0. \sqrt[]{t}+3,t\geq 0.](/latexrender/pictures/f96e0a66b59ce9763b9709d3d7e92748.png) .O deslocamento dessa particula entre os instantes t -1 t -4 ??? Substitui na xpressão e depois subtrai tudo?Fiquei perdida nos cálculos
.O deslocamento dessa particula entre os instantes t -1 t -4 ??? Substitui na xpressão e depois subtrai tudo?Fiquei perdida nos cálculos

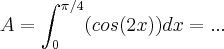
![v(x)=(dx/dt)=\sqrt[]{t}+3\Rightarrow dx=\sqrt[]{t}dt+3dt
x=\int_{t-1}^{t-4}(\sqrt[]{t}dt+3dt)=... v(x)=(dx/dt)=\sqrt[]{t}+3\Rightarrow dx=\sqrt[]{t}dt+3dt
x=\int_{t-1}^{t-4}(\sqrt[]{t}dt+3dt)=...](/latexrender/pictures/ad342cd95df77b7e4519b80b755019e6.png)
