 por elisafrombrazil » Sáb Jan 21, 2017 10:41
por elisafrombrazil » Sáb Jan 21, 2017 10:41
Utilize o Teorema do Valor Intermediário para mostrar que a equação

possui pelo menos uma solução no intervalo
![[-1,1] [-1,1]](/latexrender/pictures/d060b17b29e0dae91a1cac23ea62281a.png)
.
-
elisafrombrazil
- Usuário Ativo

-
- Mensagens: 17
- Registrado em: Sáb Dez 31, 2016 10:44
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por e8group » Qui Fev 02, 2017 15:56
por e8group » Qui Fev 02, 2017 15:56
Erro de sinal talvez no coeff. do x^2 .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por elisafrombrazil » Qui Fev 02, 2017 22:07
por elisafrombrazil » Qui Fev 02, 2017 22:07
Realmente o sinal do termo independente está trocado -> -1.
-
elisafrombrazil
- Usuário Ativo

-
- Mensagens: 17
- Registrado em: Sáb Dez 31, 2016 10:44
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por e8group » Qui Fev 02, 2017 23:38
por e8group » Qui Fev 02, 2017 23:38
Neste caso , note que a soma dos dois monomios de graus maiores é sempre

(pois

) .Como queremos que

, basta então tomar

tal que
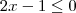
. Por exemplo ,

.
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por e8group » Qui Fev 02, 2017 23:41
por e8group » Qui Fev 02, 2017 23:41
Para obter

tal que

é trivial ! Termine ...
Obs.: Está implicito que

denota a expressão do lado esquerdo da eq. sujeito a sua correção do sinal .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Teorema do Valor Intermediário (TVI)
por jemourafer » Sex Abr 13, 2012 14:51
- 1 Respostas
- 1971 Exibições
- Última mensagem por MarceloFantini

Sáb Abr 14, 2012 00:17
Cálculo: Limites, Derivadas e Integrais
-
- Teorema do Valor Intermediário
por MCordeiro » Ter Mai 26, 2020 23:00
- 0 Respostas
- 2379 Exibições
- Última mensagem por MCordeiro

Ter Mai 26, 2020 23:00
Cálculo: Limites, Derivadas e Integrais
-
- Duvida no Teorema do valor intermediário.
por TheoFerraz » Sáb Abr 30, 2011 19:32
- 2 Respostas
- 3043 Exibições
- Última mensagem por TheoFerraz

Sáb Abr 30, 2011 19:40
Cálculo: Limites, Derivadas e Integrais
-
- [Continuidade] Problema de Valor Intermediário
por Imscatman » Seg Out 03, 2011 00:18
- 3 Respostas
- 2335 Exibições
- Última mensagem por Imscatman

Seg Out 03, 2011 02:12
Cálculo: Limites, Derivadas e Integrais
-
- Teomera do valor intermediário - exercício
por Danilo » Sáb Set 14, 2013 14:05
- 0 Respostas
- 1532 Exibições
- Última mensagem por Danilo

Sáb Set 14, 2013 14:05
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 6 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 possui pelo menos uma solução no intervalo
possui pelo menos uma solução no intervalo ![[-1,1] [-1,1]](/latexrender/pictures/d060b17b29e0dae91a1cac23ea62281a.png) .
.
 possui pelo menos uma solução no intervalo
possui pelo menos uma solução no intervalo ![[-1,1] [-1,1]](/latexrender/pictures/d060b17b29e0dae91a1cac23ea62281a.png) .
.


 (pois
(pois  ) .Como queremos que
) .Como queremos que  , basta então tomar
, basta então tomar  tal que
tal que 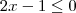 . Por exemplo ,
. Por exemplo ,  .
.
 tal que
tal que  é trivial ! Termine ...
é trivial ! Termine ...  denota a expressão do lado esquerdo da eq. sujeito a sua correção do sinal .
denota a expressão do lado esquerdo da eq. sujeito a sua correção do sinal .
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.