soluçao:
dado um triang.qquer,seja x,y,lados e b,base e h altura...
sejam
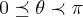 ,o angulo q. x faz com b e
,o angulo q. x faz com b e 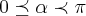 ,o angulo q. y faz com a base b...teremos entao,usando a lei dos cossenos q.:
,o angulo q. y faz com a base b...teremos entao,usando a lei dos cossenos q.: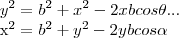

 ...
... ,logo:
,logo: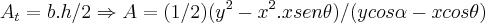 ,tomamos entao:
,tomamos entao: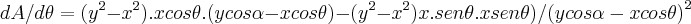 ,aqui usei a derivada do quociente...entao para:
,aqui usei a derivada do quociente...entao para: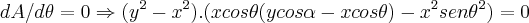
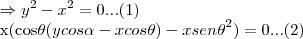
de

de
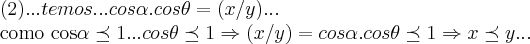
logo por
 ...cqd
...cqd

![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)