 por douglasnickson » Dom Jul 03, 2016 01:39
por douglasnickson » Dom Jul 03, 2016 01:39
Olá pessoal, estou com uma lista de exercicio da disciplina sinais e sistemas e me deparei com a seguinte questão:
se f é uma função par e contínua no intervalo [-a,a] então:
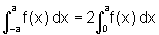
Gostaria de saber como eu faço pra chegar no resultado, se possível digam o passo a passo e quais regras eu devo usar, e fundamental saber isso na disciplina.
-
douglasnickson
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Sáb Jan 30, 2016 13:26
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Telemática
- Andamento: cursando
 por e8group » Dom Jul 03, 2016 20:52
por e8group » Dom Jul 03, 2016 20:52
Lembre que uma função f (definida num dominio simetrico ) é dita ser par se

para todo x . Faça o esboço do gráfico de alguns exemplos
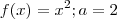
,
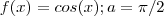
para fixar ideias ..Qual o comportamento de função continua par genérica num compacto simétrico
![[-2,2] , [-5,5], -[20,20] ou [-a,a] [-2,2] , [-5,5], -[20,20] ou [-a,a]](/latexrender/pictures/6edcd7b7de1eb7062e7418a51ab9d85a.png)
...O que significa
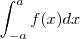
geometricamnete??? Corresponde a area com sinal da area delimitada pela gráfico da função , eixo x , e as retas verticais x = -a e x = a ... So para fixar ideias supor

.. Chame a região de R .. Assim ,
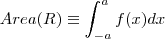
..Esta região se decompõe como união de duas regiões
cuja interseção é uma região tem medida (area) nula .. Quem são elas ??
Logo pela atividade da integral
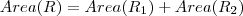
.. Observe que
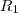
pode ser obtida reflexão como reflexão de
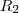
sobre o eixo y
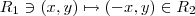
... Intuitivamente ,
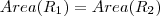
.. Logo
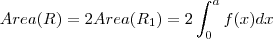
.. Isto é intuitivo e nos leva a conjeturar oq vc postou .. A prova por sua vez é bem simples .. Basta verificar que
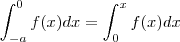
. Dica use o fato que f é par + faça uma subsituição
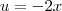
...
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por douglasnickson » Dom Jul 03, 2016 22:37
por douglasnickson » Dom Jul 03, 2016 22:37
Primeiramente valeu pelas dicas santhiago, então, a teoria eu atendi, mas não to conseguindo efetuar o passo a passo dos cálculos até chegar no resultado final, parte e separar a integral em dois intervalos ok, mas e depois o que eu devo fazer? tem alguma forma pra mim utilizar?
-
douglasnickson
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Sáb Jan 30, 2016 13:26
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Telemática
- Andamento: cursando
 por e8group » Dom Jul 03, 2016 22:53
por e8group » Dom Jul 03, 2016 22:53
Chame de
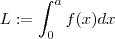
(Atenção a variável x é muda , de modo que
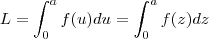
etc )
Vamos mostrar que
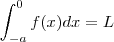
. Daí o resultado segue já que a integral de f sobre [-a,a] é a soma destas integrais .
Ora, se f é par , então f(x) = f(-x) para todo x , logo
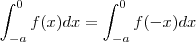
.
Agora faça uma substituição
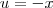
.Feito isto , verifique que (após trocar dx por -du e atualizar os limites de integração )
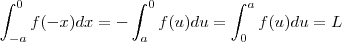
.
Obs.: Vale um resultado análogo para ímpar no lugar de par , mas o valor da integral será zero .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por douglasnickson » Dom Jul 03, 2016 23:53
por douglasnickson » Dom Jul 03, 2016 23:53
Agora acho que entendi, ai no caso no final qnd trocar o U pelo -x por ser par eu posso fazer o processo inverso e voltar o x e o -du qnd eu trocar os limites cancela o menos não eh isso?
ai voltando pra x eu somo com a outra integral e da o resultado da questão correto?
Agora vou fazer pra parte impar que também pede, o processo e o mesmo neh?
-
douglasnickson
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Sáb Jan 30, 2016 13:26
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Telemática
- Andamento: cursando
 por adauto martins » Ter Jul 05, 2016 15:25
por adauto martins » Ter Jul 05, 2016 15:25
primeiramente mostrarei q. sendo f(x) uma funçao par,teremos:
a)
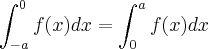
...de fato,pois
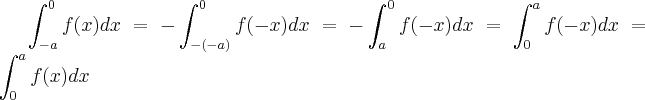
...
entao...
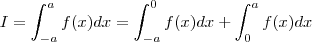
,por a)teremos entao:
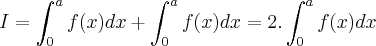
...
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [integral definida] - dúvida em exercício
 por natanaelskt » Qua Jul 02, 2014 02:13
por natanaelskt » Qua Jul 02, 2014 02:13
- 1 Respostas
- 1914 Exibições
- Última mensagem por e8group

Qua Jul 02, 2014 14:04
Cálculo: Limites, Derivadas e Integrais
-
- [Integração Definida] dúvida em integral com u.du
por Nicolas1Lane » Sáb Ago 30, 2014 20:36
- 3 Respostas
- 3386 Exibições
- Última mensagem por DanielFerreira

Dom Set 07, 2014 21:35
Cálculo: Limites, Derivadas e Integrais
-
- [calculo] dúvida - integral definida com raiz
por beel » Sex Nov 18, 2011 14:28
- 1 Respostas
- 2420 Exibições
- Última mensagem por MarceloFantini

Sex Nov 18, 2011 16:25
Cálculo: Limites, Derivadas e Integrais
-
- [Integral] Resolver Integral definida com trigonometria
por rodrigoboreli » Dom Set 07, 2014 01:02
- 1 Respostas
- 4347 Exibições
- Última mensagem por adauto martins

Sex Out 17, 2014 12:39
Cálculo: Limites, Derivadas e Integrais
-
- [Cálculo Integral] Integral Definida
por ARCS » Sáb Fev 02, 2013 21:37
- 2 Respostas
- 3681 Exibições
- Última mensagem por e8group

Sáb Fev 02, 2013 22:13
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 6 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
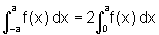

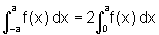

 para todo x . Faça o esboço do gráfico de alguns exemplos
para todo x . Faça o esboço do gráfico de alguns exemplos 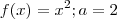 ,
, 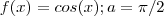 para fixar ideias ..Qual o comportamento de função continua par genérica num compacto simétrico
para fixar ideias ..Qual o comportamento de função continua par genérica num compacto simétrico ![[-2,2] , [-5,5], -[20,20] ou [-a,a] [-2,2] , [-5,5], -[20,20] ou [-a,a]](/latexrender/pictures/6edcd7b7de1eb7062e7418a51ab9d85a.png) ...O que significa
...O que significa 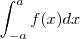 geometricamnete??? Corresponde a area com sinal da area delimitada pela gráfico da função , eixo x , e as retas verticais x = -a e x = a ... So para fixar ideias supor
geometricamnete??? Corresponde a area com sinal da area delimitada pela gráfico da função , eixo x , e as retas verticais x = -a e x = a ... So para fixar ideias supor  .. Chame a região de R .. Assim ,
.. Chame a região de R .. Assim , 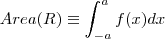 ..Esta região se decompõe como união de duas regiões
..Esta região se decompõe como união de duas regiões 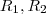 cuja interseção é uma região tem medida (area) nula .. Quem são elas ??
cuja interseção é uma região tem medida (area) nula .. Quem são elas ?? 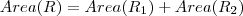 .. Observe que
.. Observe que 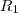 pode ser obtida reflexão como reflexão de
pode ser obtida reflexão como reflexão de 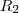 sobre o eixo y
sobre o eixo y 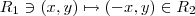 ... Intuitivamente ,
... Intuitivamente , 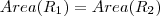 .. Logo
.. Logo 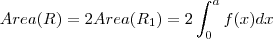 .. Isto é intuitivo e nos leva a conjeturar oq vc postou .. A prova por sua vez é bem simples .. Basta verificar que
.. Isto é intuitivo e nos leva a conjeturar oq vc postou .. A prova por sua vez é bem simples .. Basta verificar que 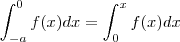 . Dica use o fato que f é par + faça uma subsituição
. Dica use o fato que f é par + faça uma subsituição 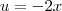 ...
...

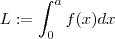 (Atenção a variável x é muda , de modo que
(Atenção a variável x é muda , de modo que 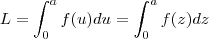 etc )
etc ) 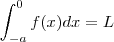 . Daí o resultado segue já que a integral de f sobre [-a,a] é a soma destas integrais .
. Daí o resultado segue já que a integral de f sobre [-a,a] é a soma destas integrais . 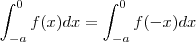 .
.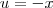 .Feito isto , verifique que (após trocar dx por -du e atualizar os limites de integração )
.Feito isto , verifique que (após trocar dx por -du e atualizar os limites de integração ) 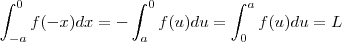 .
. 

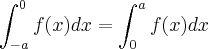 ...de fato,pois
...de fato,pois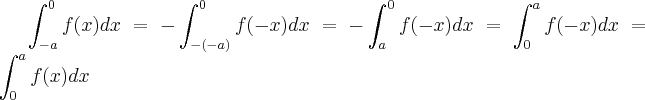 ...
...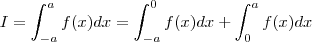 ,por a)teremos entao:
,por a)teremos entao: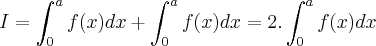 ...
...