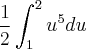por bencz » Sex Mar 18, 2016 10:42
por bencz » Sex Mar 18, 2016 10:42
Estou estudando integração, e me deparei com o seguinte exercício:
Após pegar a variável u e sua derivada,
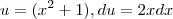
, eu coloco na integral, com os valores limites recalculados, mas eu não consigo entender o por que o

que esta fora do parenteses 'some' da integração, na proxima etapa onde eu iria colocar o

para ser integrado, eu já coloco mais o

.
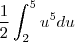
Por que, sendo que, se eu tivesse que calcular a anti-derivada do

, eu deveria colocar na equação p/ ser calculada também ?
-
bencz
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Qui Jul 14, 2011 00:21
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por anselmojr97 » Dom Mar 20, 2016 17:09
por anselmojr97 » Dom Mar 20, 2016 17:09
Olá, Bencz.
Quando você faz
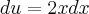
o próximo passo será achar o valor de

para substituir na integral, porque agora estará em função de

e não mais em função de

Então ficará:
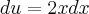
![\[ \frac{du}{2x} \] = dx \[ \frac{du}{2x} \] = dx](/latexrender/pictures/2a20e8b8283ad295135ce3f45ce3e8d0.png)
Aí você substitui na Integral.
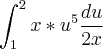
Como é tudo produto, você pode simplificar o

do numerador por o do denominador. Ficando assim:
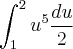
Você pode passar a constante

para fora Integral:
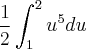
Assim você pode desenvolver o restante da Integral.
(Caso tenha alguma duvida sobre o restante do desenvolvimento, é só falar.)
Espero ter ajudado.
Abraços.
"Felizes aqueles que se divertem com problemas que educam a alma e elevam o espírito". (Fenelon)
-
anselmojr97
- Usuário Ativo

-
- Mensagens: 10
- Registrado em: Qui Set 17, 2015 21:52
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Civil
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Endomorfismo e matriz anti simetrica
por matlearn » Dom Mar 20, 2011 23:40
- 0 Respostas
- 2487 Exibições
- Última mensagem por matlearn

Dom Mar 20, 2011 23:40
Geometria Analítica
-
- [Integral] Integração por parte...
por Jessica Seno » Dom Out 14, 2012 14:37
- 3 Respostas
- 1996 Exibições
- Última mensagem por DanielFerreira

Dom Out 28, 2012 17:17
Cálculo: Limites, Derivadas e Integrais
-
- [Integral] Integração por parte
por LAZAROTTI » Ter Out 23, 2012 10:33
- 1 Respostas
- 1244 Exibições
- Última mensagem por MarceloFantini

Ter Out 23, 2012 12:03
Cálculo: Limites, Derivadas e Integrais
-
- [Integral] Integração por partes
por bencz » Sex Abr 22, 2016 16:18
- 1 Respostas
- 3690 Exibições
- Última mensagem por nakagumahissao

Sáb Abr 23, 2016 23:33
Cálculo: Limites, Derivadas e Integrais
-
- [Integração por Partes] Integral indefinida...
por luiz_henriquear » Qui Dez 22, 2011 17:40
- 1 Respostas
- 3705 Exibições
- Última mensagem por LuizAquino

Qui Dez 22, 2011 21:58
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 5 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
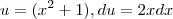 , eu coloco na integral, com os valores limites recalculados, mas eu não consigo entender o por que o
, eu coloco na integral, com os valores limites recalculados, mas eu não consigo entender o por que o  que esta fora do parenteses 'some' da integração, na proxima etapa onde eu iria colocar o
que esta fora do parenteses 'some' da integração, na proxima etapa onde eu iria colocar o  para ser integrado, eu já coloco mais o
para ser integrado, eu já coloco mais o  .
.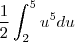
 , eu deveria colocar na equação p/ ser calculada também ?
, eu deveria colocar na equação p/ ser calculada também ?


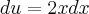 o próximo passo será achar o valor de
o próximo passo será achar o valor de  para substituir na integral, porque agora estará em função de
para substituir na integral, porque agora estará em função de  Então ficará:
Então ficará:![\[ \frac{du}{2x} \] = dx \[ \frac{du}{2x} \] = dx](/latexrender/pictures/2a20e8b8283ad295135ce3f45ce3e8d0.png)
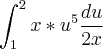
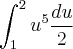
 para fora Integral:
para fora Integral: