 por Ahoush123 » Sáb Out 17, 2015 15:01
por Ahoush123 » Sáb Out 17, 2015 15:01
Boa tarde pessoal, preciso de uma ajuda. Meu professor de calculo 3 propôs uma questão extra classe que irá valer nota na próxima aula. Não consigo fazer essa questão. Se alguem puder ajuda agradeço muito
- Anexos
-

-
Ahoush123
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Sáb Out 17, 2015 14:51
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Geologia
- Andamento: cursando
 por adauto martins » Seg Out 19, 2015 12:33
por adauto martins » Seg Out 19, 2015 12:33
a)

...vou usar
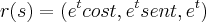
essa notaçao pra efeito de calculo...
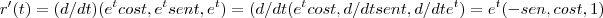
...
![{u}_{tg}=r'(t)/\left|r'(t) \right|\Rightarrow \left|r' \right|=\sqrt[]{{e}^{2t}({cost}^{2}+{sent}^{2}+1}) {u}_{tg}=r'(t)/\left|r'(t) \right|\Rightarrow \left|r' \right|=\sqrt[]{{e}^{2t}({cost}^{2}+{sent}^{2}+1})](/latexrender/pictures/9d7a9788d65c8e315af05c71d06d5d00.png)
![={e}^{t}\sqrt[]{2} ={e}^{t}\sqrt[]{2}](/latexrender/pictures/0393265483ee5d2f054c08d45cc0956c.png)
,logo...
![{u}_{tg}=(-sent/\sqrt[]{2},cost/\sqrt[]{2},1/\sqrt[]{2}) {u}_{tg}=(-sent/\sqrt[]{2},cost/\sqrt[]{2},1/\sqrt[]{2})](/latexrender/pictures/376ec9634a4416263c6a824fc47b322c.png)
...
b)
![C=\int_{0}^{3}\left|r'(t) \right|dt=\int_{0}^{3}\sqrt[]{2}{e}^{t}dt C=\int_{0}^{3}\left|r'(t) \right|dt=\int_{0}^{3}\sqrt[]{2}{e}^{t}dt](/latexrender/pictures/00ffd46aa58ddca38b671b35e00c8250.png)
...calcule!
c)

...resolva o restante...
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
 por Ahoush123 » Ter Out 20, 2015 13:08
por Ahoush123 » Ter Out 20, 2015 13:08
c)

...resolva o restante...[/quote]
Boa tarde Adalto, por favor nao consegui resolver a letra C. Estou com muitas dificuldades, agradeço muito se puder ajudar
-
Ahoush123
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Sáb Out 17, 2015 14:51
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Geologia
- Andamento: cursando
 por adauto martins » Qua Out 21, 2015 12:10
por adauto martins » Qua Out 21, 2015 12:10
temos q.
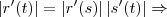
cada coordenada do vetor
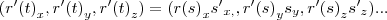
na base canonica do

,a saber
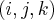
...
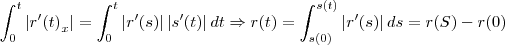

...o mesmo faz-se pra os eixos y,z...agora e determinar

...foi dado somente t=0,
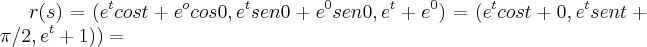
=
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
 por adauto martins » Qua Out 21, 2015 14:55
por adauto martins » Qua Out 21, 2015 14:55
uma correçao...
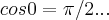
entao:

...
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Intervalo de Classe
por Walquiria » Qui Dez 01, 2011 18:49
- 1 Respostas
- 1963 Exibições
- Última mensagem por Neperiano

Sex Dez 02, 2011 14:16
Estatística
-
- [Estatistica] Tabela e intervalo de classe
por jjforums » Seg Jun 25, 2012 17:21
- 2 Respostas
- 3869 Exibições
- Última mensagem por jjforums

Seg Jun 25, 2012 18:08
Estatística
-
- [Cálculo]classe da curva, significado
por Camolas » Sex Mai 31, 2013 14:51
- 0 Respostas
- 1218 Exibições
- Última mensagem por Camolas

Sex Mai 31, 2013 14:51
Cálculo: Limites, Derivadas e Integrais
-
- [Questão POSCOMP 2011] Ajuda para interpretar questão
por hlustosa » Dom Jul 29, 2012 14:54
- 3 Respostas
- 12986 Exibições
- Última mensagem por hlustosa

Seg Jul 30, 2012 01:13
Funções
-
- Questão de P.A.
por mushthielv » Seg Ago 17, 2009 12:21
- 2 Respostas
- 10966 Exibições
- Última mensagem por Elcioschin

Ter Ago 18, 2009 08:54
Progressões
Usuários navegando neste fórum: Nenhum usuário registrado e 12 visitantes
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



 ...vou usar
...vou usar 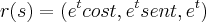 essa notaçao pra efeito de calculo...
essa notaçao pra efeito de calculo...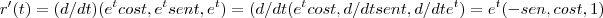 ...
...![{u}_{tg}=r'(t)/\left|r'(t) \right|\Rightarrow \left|r' \right|=\sqrt[]{{e}^{2t}({cost}^{2}+{sent}^{2}+1}) {u}_{tg}=r'(t)/\left|r'(t) \right|\Rightarrow \left|r' \right|=\sqrt[]{{e}^{2t}({cost}^{2}+{sent}^{2}+1})](/latexrender/pictures/9d7a9788d65c8e315af05c71d06d5d00.png)
![={e}^{t}\sqrt[]{2} ={e}^{t}\sqrt[]{2}](/latexrender/pictures/0393265483ee5d2f054c08d45cc0956c.png) ,logo...
,logo...![{u}_{tg}=(-sent/\sqrt[]{2},cost/\sqrt[]{2},1/\sqrt[]{2}) {u}_{tg}=(-sent/\sqrt[]{2},cost/\sqrt[]{2},1/\sqrt[]{2})](/latexrender/pictures/376ec9634a4416263c6a824fc47b322c.png) ...
...![C=\int_{0}^{3}\left|r'(t) \right|dt=\int_{0}^{3}\sqrt[]{2}{e}^{t}dt C=\int_{0}^{3}\left|r'(t) \right|dt=\int_{0}^{3}\sqrt[]{2}{e}^{t}dt](/latexrender/pictures/00ffd46aa58ddca38b671b35e00c8250.png) ...calcule!
...calcule! ...resolva o restante...
...resolva o restante...
 ...resolva o restante...[/quote]
...resolva o restante...[/quote]
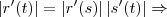 cada coordenada do vetor
cada coordenada do vetor 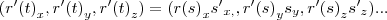 na base canonica do
na base canonica do  ,a saber
,a saber 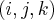 ...
...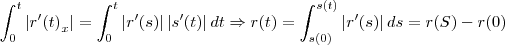
 ...o mesmo faz-se pra os eixos y,z...agora e determinar
...o mesmo faz-se pra os eixos y,z...agora e determinar  ...foi dado somente t=0,
...foi dado somente t=0,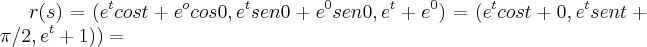 =
=
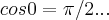 entao:
entao: ...
...
