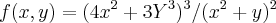por michellepoubel » Qua Set 23, 2015 12:19
Bom dia.
Estou levando uma surra destas duas questões do meu exercício, se alguém puder me ajudar como eu soluciono isso eu agradeço.
A letra b eu comecei fazendo usando a regra do quociente e depois tentei resolvendo os produtos notáveis, porém não tenho certeza do que estou fazendo..kkk A letra A nem sem como começar.
Letra a)
![f(x,y)=\sqrt[5]{x^3}/\sqrt[7]{y^2}](/latexrender/pictures/76789d58ae1bdcb77f2d503eeaeb2dd9.png "f(x,y)=\sqrt[5]{x^3}/\sqrt[7]{y^2}")
Letra b)
-
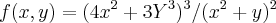
michellepoubel
- Novo Usuário
-
- Mensagens: 1
- Registrado em: Qua Set 23, 2015 11:53
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
por killerkm » Seg Set 28, 2015 18:11
-
killerkm
- Novo Usuário
-
- Mensagens: 2
- Registrado em: Seg Set 28, 2015 17:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Civil
- Andamento: cursando
por killerkm » Seg Set 28, 2015 18:21
Lembre que o y permanece como uma constante na questão a), tem que acrescentar na resposta final.
-
killerkm
- Novo Usuário
-
- Mensagens: 2
- Registrado em: Seg Set 28, 2015 17:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Civil
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Derivadas parciais de segunda ordem
por Victor Mello » Sáb Fev 22, 2014 14:49
- 2 Respostas
- 1274 Exibições
- Última mensagem por Victor Mello
Dom Fev 23, 2014 01:49
Cálculo: Limites, Derivadas e Integrais
-
- EDO de Segunda Ordem
por OtavioBonassi » Ter Nov 15, 2011 11:45
- 0 Respostas
- 1184 Exibições
- Última mensagem por OtavioBonassi
Ter Nov 15, 2011 11:45
Sistemas de Equações
-
- derivada de segunda ordem
por lgbmp » Sex Set 03, 2010 19:25
- 2 Respostas
- 2914 Exibições
- Última mensagem por lgbmp
Seg Set 06, 2010 13:35
Cálculo: Limites, Derivadas e Integrais
-
- [Derivada de segunda ordem]
por spektroos » Sáb Nov 24, 2012 23:43
- 2 Respostas
- 2091 Exibições
- Última mensagem por spektroos
Dom Nov 25, 2012 02:39
Cálculo: Limites, Derivadas e Integrais
-
- [Derivada de segunda ordem]
por spektroos » Sáb Nov 24, 2012 23:48
- 1 Respostas
- 1448 Exibições
- Última mensagem por e8group
Dom Nov 25, 2012 10:12
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
zig - Sex Set 23, 2011 13:57
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png "{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}")
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png "{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}")
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
Vennom - Sex Set 23, 2011 21:41
zig escreveu:
Rpz, o negócio é o seguinte:
Quando você tem uma potência negativa, tu deve inverter a base dela. Por exemplo:
Então pense o seguinte: a fração geratriz de 0,05 é
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
Veja:
![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png "{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}")
A raiz quadrada de vinte, você acha fácil, né?
Espero ter ajudado.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:23
Nós podemos simplificar, um pouco,
da seguinte forma:
.
É isso.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:24
Nós podemos simplificar, um pouco,
da seguinte forma:
.
É isso.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
