A racionalização foi feita daquela forma por causa das propriedades da radiciação e da potenciação. Ou seja, na potenciação, quando multiplicamos um número de base x por exemplo, elevado a algum número e outro com base também x elevado a outro número qualquer, mantemos a base e somamos os expoentes.
Para a radiciação, existe uma propriedade que diz que quando temos a raiz 'n' de algum número elevado à um expoente 'a', podemos reescrever esta raiz em forma de fração, onde, neste caso ficaria a/n.
Vou te dar alguns exemplos:
1) Potenciação:

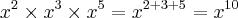
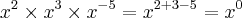
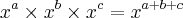
2) Radiciação:
![\sqrt[2]{{3}^{5}} = {3}^{\frac{5}{2}} \sqrt[2]{{3}^{5}} = {3}^{\frac{5}{2}}](/latexrender/pictures/5d12e362adbb81655f6180cb85404f0a.png)
![\sqrt[4]{{9}^{7}} = {9}^{\frac{7}{4}} \sqrt[4]{{9}^{7}} = {9}^{\frac{7}{4}}](/latexrender/pictures/6eb26a1d99d84cabfcab29e330687634.png)
![\sqrt[4]{{x}^{7}} = {x}^{\frac{7}{4}} \sqrt[4]{{x}^{7}} = {x}^{\frac{7}{4}}](/latexrender/pictures/0e574cf3ed6feda4c904597f4bb003e9.png)
![\sqrt[3]{x} = {x}^{\frac{1}{3}} \sqrt[3]{x} = {x}^{\frac{1}{3}}](/latexrender/pictures/7e4462eb93c9e4d2d5c18e05c40b0bd4.png)
![\sqrt[2]{x} = {x}^{\frac{1}{2}} \sqrt[2]{x} = {x}^{\frac{1}{2}}](/latexrender/pictures/0b0310156bf79f77000b77c6b128b24d.png)
3) Juntando a Radiciação e a Potenciação ficará (O último é o caso da nossa racionalização que foi feita) -
OBSERVAÇÃO IMPORTANTE! - Isto que estou explicando somente é válido para MULTIPLICAÇÃO de radicais de Índices e radicandos IGUAIS:![\sqrt[3]{{x}^{2}} \times \sqrt[3]{{x}^{5}}= {x}^{\frac{2}{3}} \times {x}^{\frac{5}{3}} = {x}^{\frac{2}{3} + \frac{5}{3}}={x}^{\frac{7}{3}} = \sqrt[3]{{x}^{7}} \sqrt[3]{{x}^{2}} \times \sqrt[3]{{x}^{5}}= {x}^{\frac{2}{3}} \times {x}^{\frac{5}{3}} = {x}^{\frac{2}{3} + \frac{5}{3}}={x}^{\frac{7}{3}} = \sqrt[3]{{x}^{7}}](/latexrender/pictures/97a89e9fcb256797909f8c5f4436d834.png)
Primeiramente:
![\sqrt[n]{a} \sqrt[n]{a}](/latexrender/pictures/bf7ff33f3b129b15c06203d60f007807.png)
'n' se chama "Índice", 'a' é radicando e o conjunto todo é chamado de radical.
Quando temos o mesmo índice (veja o exemplo dado onde o índice é o número 3) e o radicando é o mesmo (no caso do exemplo, o radicando é o 'x'), então, podemos diretamente escrever o radical usando o mesmo índice (3), o mesmo radicando (x) e finalmente, usando a propriedade da multiplicação de potências, somar os expoentes.
Veja mais exemplos:
![\sqrt[5]{{2}^{43}} \times \sqrt[5]{{2}^{3}} = \sqrt[5]{{2}^{43+3}} = \sqrt[5]{{2}^{46}} \sqrt[5]{{2}^{43}} \times \sqrt[5]{{2}^{3}} = \sqrt[5]{{2}^{43+3}} = \sqrt[5]{{2}^{46}}](/latexrender/pictures/8d785a7fd9a92f92af6b1d3f81b017cc.png)
![\sqrt[5]{{x}^{43}} \times \sqrt[5]{{x}^{3}} = \sqrt[5]{{x}^{43+3}} = \sqrt[5]{{x}^{46}} \sqrt[5]{{x}^{43}} \times \sqrt[5]{{x}^{3}} = \sqrt[5]{{x}^{43+3}} = \sqrt[5]{{x}^{46}}](/latexrender/pictures/b61eac1ee9e46d58837f044ff1864e1e.png)
Finalmente, respondendo agora sua pergunta, para podermos "eliminar" a raiz que estava no denominador, precisaríamos multiplicar por algo que fizesse com que a raiz desaparecesse. Como tínhamos:
![3\sqrt[3]{x} 3\sqrt[3]{x}](/latexrender/pictures/0af595c16ed333f4e8a4c8b42fc2aac5.png)
no denominador, teríamos que encontrar 'algo' que se multiplicássemos por ele faríamos com que a raiz 'desaparecesse'. Assim, para que a raiz desapareça teríamos que encontrar alguma coisa que tivesse o mesmo índice, o mesmo radicando, mas cuja
SOMA dos expoentes fizesse com o expoente se tornasse 3 pois:
![3\sqrt[3]{x} \times \sqrt[3]{{x}^{2}} = 3\sqrt[3]{{x}^{3}} = 3{x}^{\frac{3}{3}} = 3x^1 = 3x 3\sqrt[3]{x} \times \sqrt[3]{{x}^{2}} = 3\sqrt[3]{{x}^{3}} = 3{x}^{\frac{3}{3}} = 3x^1 = 3x](/latexrender/pictures/536d94294953e249e1f08c1a4c2a93b4.png)
Como não podemos apenas multiplicar o denominador por
![\sqrt[3]{{x}^{2}} \sqrt[3]{{x}^{2}}](/latexrender/pictures/bc3929ea927ff7f7af8e6c1c5a1213b0.png)
porque mudaria o resultado final, temos então que multiplicar e dividir por ele mesmo (que na realidade seria multiplicar por 1, o que não muda o resultado em nada por estarmos multiplicando um número dividido por ele mesmo), então multipliquei em cima e embaixo (numerador e denominador) por:
![\frac{\sqrt[3]{{x}^{2}}}{\sqrt[3]{{x}^{2}}} \frac{\sqrt[3]{{x}^{2}}}{\sqrt[3]{{x}^{2}}}](/latexrender/pictures/a763aec51cb6bf1311053ff1b99d0de1.png)
Espero que tenha compreendido.
Eu faço a diferença. E você?
Do Poema: Quanto os professores "fazem"?
De Taylor Mali
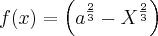
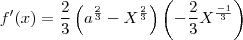 , mas apartir daí não consigo chegar na simplificação correta, que segundo o gabarito seria:
, mas apartir daí não consigo chegar na simplificação correta, que segundo o gabarito seria:![f'(x)=\sqrt[]{\sqrt[3]{\frac{{a}^{2}}{{x}^{2}}-1}} f'(x)=\sqrt[]{\sqrt[3]{\frac{{a}^{2}}{{x}^{2}}-1}}](/latexrender/pictures/122c24a32efbd3d16517a7472bf2d414.png)

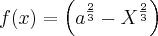
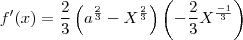 , mas apartir daí não consigo chegar na simplificação correta, que segundo o gabarito seria:
, mas apartir daí não consigo chegar na simplificação correta, que segundo o gabarito seria:![f'(x)=\sqrt[]{\sqrt[3]{\frac{{a}^{2}}{{x}^{2}}-1}} f'(x)=\sqrt[]{\sqrt[3]{\frac{{a}^{2}}{{x}^{2}}-1}}](/latexrender/pictures/122c24a32efbd3d16517a7472bf2d414.png)

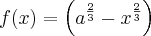
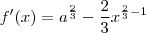
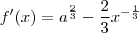

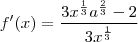
![f'(x)= \frac{3\sqrt[3]{x}\sqrt[3]{{a}^{2}} - 2}{3\sqrt[3]{x}} f'(x)= \frac{3\sqrt[3]{x}\sqrt[3]{{a}^{2}} - 2}{3\sqrt[3]{x}}](/latexrender/pictures/ffba229f1324bf951ab6ab286bc0f3d0.png)
![f'(x)= \frac{3\sqrt[3]{x{a}^{2}}- 2}{3\sqrt[3]{x}} f'(x)= \frac{3\sqrt[3]{x{a}^{2}}- 2}{3\sqrt[3]{x}}](/latexrender/pictures/02a87aa44a0bd42ed3b5a185d5b12864.png)
![f'(x)= \frac{3\sqrt[3]{x{a}^{2}}- 2}{3\sqrt[3]{x}} \cdot \frac{\sqrt[3]{x^2}}{\sqrt[3]{x^2}} f'(x)= \frac{3\sqrt[3]{x{a}^{2}}- 2}{3\sqrt[3]{x}} \cdot \frac{\sqrt[3]{x^2}}{\sqrt[3]{x^2}}](/latexrender/pictures/0b82a27a8ae1990e99dd4a2925051020.png)
![f'(x)= \frac{3x\sqrt[3]{a^2} - 2}{3x} f'(x)= \frac{3x\sqrt[3]{a^2} - 2}{3x}](/latexrender/pictures/4067e01a98de5abfaf8dea8b447d5111.png)
![f'(x)= \sqrt[3]{a^2} - \frac{2}{3x} f'(x)= \sqrt[3]{a^2} - \frac{2}{3x}](/latexrender/pictures/a4353f4c5a77111b6af12f39ba0e6b7d.png)

![\frac{\sqrt[3]{{x}^{2}}}{\sqrt[3]{{x}^{2}}} \frac{\sqrt[3]{{x}^{2}}}{\sqrt[3]{{x}^{2}}}](/latexrender/pictures/a763aec51cb6bf1311053ff1b99d0de1.png) ao invés de racionalizar por
ao invés de racionalizar por ![\frac{\sqrt[3]{x}}{\sqrt[3]{x}} \frac{\sqrt[3]{x}}{\sqrt[3]{x}}](/latexrender/pictures/11da322cfe6db8d2ebfaa26339f3a4c5.png) ?
?

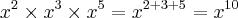
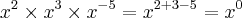
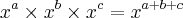
![\sqrt[2]{{3}^{5}} = {3}^{\frac{5}{2}} \sqrt[2]{{3}^{5}} = {3}^{\frac{5}{2}}](/latexrender/pictures/5d12e362adbb81655f6180cb85404f0a.png)
![\sqrt[4]{{9}^{7}} = {9}^{\frac{7}{4}} \sqrt[4]{{9}^{7}} = {9}^{\frac{7}{4}}](/latexrender/pictures/6eb26a1d99d84cabfcab29e330687634.png)
![\sqrt[4]{{x}^{7}} = {x}^{\frac{7}{4}} \sqrt[4]{{x}^{7}} = {x}^{\frac{7}{4}}](/latexrender/pictures/0e574cf3ed6feda4c904597f4bb003e9.png)
![\sqrt[3]{x} = {x}^{\frac{1}{3}} \sqrt[3]{x} = {x}^{\frac{1}{3}}](/latexrender/pictures/7e4462eb93c9e4d2d5c18e05c40b0bd4.png)
![\sqrt[2]{x} = {x}^{\frac{1}{2}} \sqrt[2]{x} = {x}^{\frac{1}{2}}](/latexrender/pictures/0b0310156bf79f77000b77c6b128b24d.png)
![\sqrt[3]{{x}^{2}} \times \sqrt[3]{{x}^{5}}= {x}^{\frac{2}{3}} \times {x}^{\frac{5}{3}} = {x}^{\frac{2}{3} + \frac{5}{3}}={x}^{\frac{7}{3}} = \sqrt[3]{{x}^{7}} \sqrt[3]{{x}^{2}} \times \sqrt[3]{{x}^{5}}= {x}^{\frac{2}{3}} \times {x}^{\frac{5}{3}} = {x}^{\frac{2}{3} + \frac{5}{3}}={x}^{\frac{7}{3}} = \sqrt[3]{{x}^{7}}](/latexrender/pictures/97a89e9fcb256797909f8c5f4436d834.png)
![\sqrt[n]{a} \sqrt[n]{a}](/latexrender/pictures/bf7ff33f3b129b15c06203d60f007807.png)
![\sqrt[5]{{2}^{43}} \times \sqrt[5]{{2}^{3}} = \sqrt[5]{{2}^{43+3}} = \sqrt[5]{{2}^{46}} \sqrt[5]{{2}^{43}} \times \sqrt[5]{{2}^{3}} = \sqrt[5]{{2}^{43+3}} = \sqrt[5]{{2}^{46}}](/latexrender/pictures/8d785a7fd9a92f92af6b1d3f81b017cc.png)
![\sqrt[5]{{x}^{43}} \times \sqrt[5]{{x}^{3}} = \sqrt[5]{{x}^{43+3}} = \sqrt[5]{{x}^{46}} \sqrt[5]{{x}^{43}} \times \sqrt[5]{{x}^{3}} = \sqrt[5]{{x}^{43+3}} = \sqrt[5]{{x}^{46}}](/latexrender/pictures/b61eac1ee9e46d58837f044ff1864e1e.png)
![3\sqrt[3]{x} 3\sqrt[3]{x}](/latexrender/pictures/0af595c16ed333f4e8a4c8b42fc2aac5.png)
![3\sqrt[3]{x} \times \sqrt[3]{{x}^{2}} = 3\sqrt[3]{{x}^{3}} = 3{x}^{\frac{3}{3}} = 3x^1 = 3x 3\sqrt[3]{x} \times \sqrt[3]{{x}^{2}} = 3\sqrt[3]{{x}^{3}} = 3{x}^{\frac{3}{3}} = 3x^1 = 3x](/latexrender/pictures/536d94294953e249e1f08c1a4c2a93b4.png)
![\sqrt[3]{{x}^{2}} \sqrt[3]{{x}^{2}}](/latexrender/pictures/bc3929ea927ff7f7af8e6c1c5a1213b0.png)
![\frac{\sqrt[3]{{x}^{2}}}{\sqrt[3]{{x}^{2}}} \frac{\sqrt[3]{{x}^{2}}}{\sqrt[3]{{x}^{2}}}](/latexrender/pictures/a763aec51cb6bf1311053ff1b99d0de1.png)

