 por johnatta » Ter Abr 07, 2015 17:41
por johnatta » Ter Abr 07, 2015 17:41
Calcule caso exista. Se não justifique
lim | x- 1|/x-1
x-->1^+
lim |x-1|/x-1
x-->1^-
lim |x-1|/x-1
x-->1
lim raiz quadrada de x
x-->0
-
johnatta
- Usuário Ativo

-
- Mensagens: 16
- Registrado em: Ter Abr 07, 2015 17:14
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por adauto martins » Qua Abr 08, 2015 20:20
por adauto martins » Qua Abr 08, 2015 20:20
1)



o limite p/
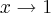
,nao existe,como mostramos anteriormente...tende p/ valores distintos (1,-1)
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
 por johnatta » Sex Abr 10, 2015 21:44
por johnatta » Sex Abr 10, 2015 21:44
Nesse caso, vc cortou direto ou foi chutando valores maiores e depois menores que 1 ? Ou tanto faz ? Grato !
-
johnatta
- Usuário Ativo

-
- Mensagens: 16
- Registrado em: Ter Abr 07, 2015 17:14
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por adauto martins » Seg Abr 13, 2015 19:26
por adauto martins » Seg Abr 13, 2015 19:26
meu caro jonathan,
matematica nao eh chute,eh logica,e uso da teoria pra resolver exercicios...

...
ao passar o limite,deve-se retirar os modulos...
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Cálculo: Limites, Derivadas e Integrais] Cálculo de limites
por jeferson lopes » Ter Mar 26, 2013 08:49
- 2 Respostas
- 5555 Exibições
- Última mensagem por jeferson lopes

Ter Mar 26, 2013 11:52
Cálculo: Limites, Derivadas e Integrais
-
- [limites] exercicio de calculo envolvendo limites
por lucasdemirand » Qua Jul 10, 2013 00:45
- 1 Respostas
- 4802 Exibições
- Última mensagem por e8group

Sáb Jul 20, 2013 13:08
Cálculo: Limites, Derivadas e Integrais
-
- [Cálculo 2 - Limites] Existência de Limites
por Piva » Seg Abr 16, 2012 11:29
- 0 Respostas
- 5439 Exibições
- Última mensagem por Piva

Seg Abr 16, 2012 11:29
Cálculo: Limites, Derivadas e Integrais
-
- cálculo de limites
por Hansegon » Seg Ago 25, 2008 11:29
- 2 Respostas
- 59825 Exibições
- Última mensagem por Guill

Dom Abr 08, 2012 16:03
Cálculo: Limites, Derivadas e Integrais
-
- Calculo de limites
por Emanuel_27 » Sáb Nov 01, 2008 01:57
- 3 Respostas
- 7134 Exibições
- Última mensagem por Molina

Qui Abr 09, 2009 22:47
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.






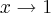 ,nao existe,como mostramos anteriormente...tende p/ valores distintos (1,-1)
,nao existe,como mostramos anteriormente...tende p/ valores distintos (1,-1)

 ...
...
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.