


 centrada na origem. Portanto, a forma de simetria é polar. Assim, o mais indicado é utilizar coordenadas polares!
centrada na origem. Portanto, a forma de simetria é polar. Assim, o mais indicado é utilizar coordenadas polares!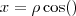

 (circunferência centrada na origem) você obtém
(circunferência centrada na origem) você obtém 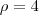 .
.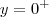 representam, no nosso sistema de coordenadas,
representam, no nosso sistema de coordenadas,  de modo que
de modo que 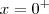 a norte representam
a norte representam  e a esquerda de
e a esquerda de 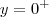 representam
representam  .
. e
e  .
. a ser integrada será substituída por
a ser integrada será substituída por  e o elemento de área
e o elemento de área 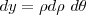 .
.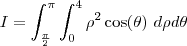 .
.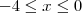 e
e 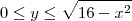 pois a integral
pois a integral 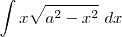
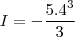 .
.


 . Daí, como
. Daí, como  então,
então,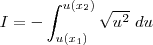 .
.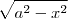 é positiva, então
é positiva, então  e , daí,
e , daí, 



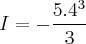 , fiz de várias maneiras porém não consigo desenvolver, não consigo chegar a esse resultado, esse é o problema amigo...
, fiz de várias maneiras porém não consigo desenvolver, não consigo chegar a esse resultado, esse é o problema amigo...

 . Daí, como
. Daí, como  então,
então, .
.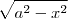 é positiva, então
é positiva, então  e , daí,
e , daí, 
 e
e  então
então  e
e  . Assim,
. Assim, 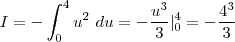


Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 12 visitantes


 , avisa que eu resolvo.
, avisa que eu resolvo.

